
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣3,数列{bn}的前n项和Tn满足 ![]() =
= ![]() +1且b1=1.
+1且b1=1.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Pn;
,求数列{cn}的前n项和Pn;
(3)数列{Sn}中是否存在不同的三项Sp , Sq , Sr , 使这三项恰好构成等差数列?若存在,求出p,q,r的关系;若不存在,请说明理由.
【答案】
(1)解:∵2Sn=3an﹣3,
当n=1时,2a1=3a1﹣3,
∴a1=3.
当n≥2时,2an=2Sn﹣2Sn﹣1=(3an﹣3)﹣(3an﹣1﹣3),
∴an=3an﹣1.
∴{an}是以3为首项,以3为公比的等比数列.
∴an=3n.
∵ ![]() =
= ![]() +1,
+1,
∴ ![]() ﹣
﹣ ![]() =1,
=1,
∴{ ![]() }是以1为首项,以1为公差的等差数列,
}是以1为首项,以1为公差的等差数列,
∴ ![]() =n.即Tn=n2.
=n.即Tn=n2.
当n≥2时,bn=Tn﹣Tn﹣1=n2﹣(n﹣1)2=2n﹣1.
当n=1时,上式仍成立,
∴bn=2n﹣1.
(2)解:由(1)知cn= ![]() .
.
∴Pn=c1+c2+c3+…+cn= ![]() +
+ ![]() +
+ ![]() +
+ ![]() …+
…+ ![]() .①
.①
∴ ![]() Pn=
Pn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() .②
.②
①﹣②得: ![]() Pn=
Pn= ![]() +2
+2 ![]() +2
+2 ![]() +2
+2 ![]() +…+2
+…+2 ![]() ﹣
﹣ ![]() =
= ![]() +2
+2 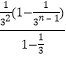 ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() .
.
∴Pn=1﹣ ![]() .
.
(3)解:由(1)知{an}是以3为首项,以3为公比的等比数列,
∴Sn= ![]() =
= ![]() .
.
假设数列{Sn}中存在不同的三项Sp,Sq,Sr,使这三项恰好构成等差数列,
∴Sp+Sr=2Sq.即 ![]() +
+ ![]() =3q+1﹣3.
=3q+1﹣3.
∴ ![]() .即3p+3r=23q.
.即3p+3r=23q.
则3p(1+3r﹣p)=23q.
∴ ![]() ,
,
∴p=q=r.与假设矛盾、
∴数列{Sn}中不存在不同的三项Sp,Sq,Sr,使这三项恰好构成等差数列
【解析】(1)根据an= ![]() 得出{an}为等比数列,由{
得出{an}为等比数列,由{ ![]() }为等差数列求出{
}为等差数列求出{ ![]() }的通项公式,再得出数列{an},{bn}的通项公式;(2)使用错位相减法求和;(3)假设存在三项成等差数列,根据等差数列的性质化简得出矛盾.
}的通项公式,再得出数列{an},{bn}的通项公式;(2)使用错位相减法求和;(3)假设存在三项成等差数列,根据等差数列的性质化简得出矛盾.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系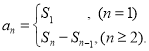 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】为调查高中生的数学成绩与学生自主学习时间之间的相关关系,长郡中学数学教师对新入学的45名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有19人,余下的人中,在高三模拟考试中数学平均成绩不足120分的占![]() ,统计成绩后,得到如下的
,统计成绩后,得到如下的![]() 列联表:
列联表:
分数大于等于120分 | 分数不足120分 | 合计 | |
周做题时间不少于15小时 | 4 | 19 | |
周做题时间不足15小时 | |||
合计 | 45 |
(1)请完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
(2)(ⅰ)按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
(ⅱ)若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
|
|
|
|
|
|
|
|
附: 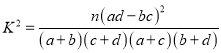
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=AD=1,E为CD中点. 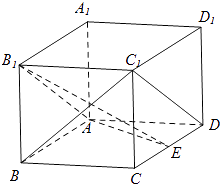
(1)求证:C1D∥平面AB1E;
(2)求证:BC1⊥B1E;
(3)若AB= ![]() ,求二面角E﹣AB1﹣B的正切值.
,求二面角E﹣AB1﹣B的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a2x+ ![]() (a,b,c为常数,且a>0,c>0).
(a,b,c为常数,且a>0,c>0).
(1)当a=1,b=0时,求证:|f(x)|≥2c;
(2)当b=1时,如果对任意的x>1都有f(x)>a恒成立,求证:a+2c>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为 . 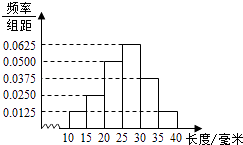
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽淮南二模】随着社会发展,淮北市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从淮北市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
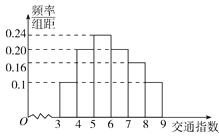
(I)据此直方图估算交通指数T∈[4,8)时的中位数和平均数;
(II)据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏. 
(1)若∠APQ=15°,AP与AQ两处围墙长度和为100( ![]() +1)米,求栅栏PQ的长;
+1)米,求栅栏PQ的长;
(2)已知AB,AC的长度均大于200米,若水果园APQ面积为2500 ![]() 平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小?
平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为6.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx﹣2相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com