
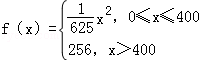 ��
��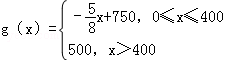 ��
��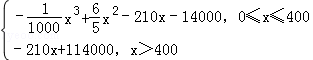 ��
��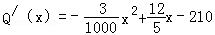 ��
��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012���㽭ʡ����ʮУ������߶���һѧ����ĩ������ѧ�Ծ����Ŀƣ� ���ͣ������
����ij˽Ӫ��˾����һ�ֲ�Ʒ����������������֪�������ò�Ʒÿ��Ĺ̶��ɱ�Ϊ14000Ԫ��ÿ����һ���ò�Ʒ���ɱ�����210Ԫ����֪�ò�Ʒ����������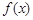 �����
�����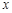 ֮��Ĺ�ϵʽΪ
֮��Ĺ�ϵʽΪ
 ��ÿ����Ʒ���ۼ�
��ÿ����Ʒ���ۼ�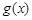 �����
�����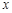 ֮��Ĺ�ϵʽΪ
֮��Ĺ�ϵʽΪ
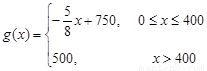 ��
��
����д���ù�˾������������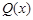 �����
�����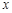 ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
������Ҫʹ���������������ÿ����������ټ���Ʒ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012-2013ѧ�����������ѧ�������ϣ�8���¿���ѧ�Ծ������ƣ��������棩 ���ͣ������
 ��ÿ����Ʒ���ۼ�g��x�������x֮��Ĺ�ϵʽΪ
��ÿ����Ʒ���ۼ�g��x�������x֮��Ĺ�ϵʽΪ ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011ѧ���㽭ʡ������ʮУ������߶����ϣ���ĩ��ѧ�Ծ����Ŀƣ��������棩 ���ͣ������
 ��ÿ����Ʒ���ۼ�g��x�������x֮��Ĺ�ϵʽΪ
��ÿ����Ʒ���ۼ�g��x�������x֮��Ĺ�ϵʽΪ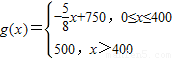 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2008��㶫ʡ��ɽ�и߿���ѧһģ�Ծ������ƣ��������棩 ���ͣ������
 ��ÿ����Ʒ���ۼ�g��x�������x֮��Ĺ�ϵʽΪ
��ÿ����Ʒ���ۼ�g��x�������x֮��Ĺ�ϵʽΪ ��
���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com