【题目】过椭圆
的右焦点F作两条相互垂直的直线分别交椭圆于A，B，C，D四点，则
的值为（ ）
A. 
B. 
C. 1 D. 
【答案】D
【解析】
当直线AB的斜率不存在时，AB：x=1，推导出
=
；当直线AB的斜率存在时，设AB：y=k（x﹣1）（k≠0），CD：y=﹣
（x﹣1）．分别利用弦长公式求出|AB|、|CD|的长度，由此能推导出=为定值．
由椭圆
，得椭圆的右焦点为F（1，0），
当直线AB的斜率不存在时，AB：x=1，
则CD：y=0．此时|AB|=3，|CD|=4，
则=
；
当直线AB的斜率存在时，
设AB：y=k（x﹣1）（k≠0），则 CD：y=﹣（x﹣1）．
又设点A（x1，y1），B（x2，y2）．
联立方程组
，
消去y并化简得（4k2+3）x2﹣8k2x+4k2﹣12=0，
∴
，
∴|AB|=
=
=
，
由题知，直线CD的斜率为﹣，
同理可得|CD|=
．
∴=
为定值．
故选：D．
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案科目：高中数学 来源： 题型：
【题目】设函数f（x）=1﹣ 
，g（x）=ln（ax2﹣3x+1），若对任意的x1∈[0，+∞），都存在x2∈R，使得f（x1）=g（x2）成立，则实数a的最大值为（ ）
A.2
B.
C.4
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（1）双曲线
的离心率为_____________
（2）点P是椭圆
上一点，
分别是椭圆的左、右焦点，若
，则
的大小______ ．
（3）如果
是抛物线y2=4x上的点，它们的横坐标依次为
，F是抛物线的焦点，若
则
_______________．
（4）若x,y满足约束条件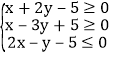
,则z=x2+y2的最大值为______________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集为[﹣1，1]．
（1）求m的值；
（2）若a，b，c∈R，且 
=m，求证：a+2b+3c≥9．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设p：不等式x2+（m﹣1）x+1＞0的解集为R；q：x∈（0，+∞），m≤x+ 
恒成立．若“p且q”为假命题，“p或q”为真命题，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知椭圆
的离心率为
，且过点
.
（1）求
的方程；
（2）若动点
在直线
上，过
作直线交椭圆
于
两点，使得
，再过
作直线
，证明：直线
恒过定点，并求出该定点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}前n项和为Sn ， 满足Sn=2an﹣2n（n∈N*）．
（1）证明：{an+2}是等比数列，并求{an}的通项公式；
（2）数列{bn}满足bn=log2（an+2），Tn为数列{ 
}的前n项和，若Tn＜a对正整数a都成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ex（x2﹣a），a∈R．
（1）当a=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）若函数f（x）在（﹣3，0）上单调递减，试求a的取值范围；
（3）若函数f（x）的最小值为﹣2e，试求a的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
