
已知复数z=(2+i)m2--2(1-i).当实数m取什么值时,复数z是:
(1)虚数;(2)纯虚数;(3)复平面内第二、四象限角平分线上的点对应的复数?
(1) m≠2且m≠1时,z为虚数;(2)m=-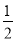 时,z为纯虚数;(3) m=0或m=2时, z为复平面内第二、四象限角平分线上的点对应的复数.
时,z为纯虚数;(3) m=0或m=2时, z为复平面内第二、四象限角平分线上的点对应的复数.
【解析】
试题分析:(1)复数z可表示为z=(2+i)m2﹣2(1﹣i)=2m2﹣2+(m2+2)i.只需令m2+2≠0即可;(2)只需2m2﹣2=0,且m2+2≠0即可;(3)只需2m2﹣2=﹣(m2+2)即可.
试题解析:由于m∈R,复数z可表示为z=(2+i)m2-3m(1+i)-2(1-i)=(2m2-3m-2)+(m2-3m+2)i.
(1)当m2-3m+2≠0,即m≠2且m≠1时,z为虚数.(3分)
(2)当即m=-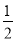 时,z为纯虚数.(3分)
时,z为纯虚数.(3分)
(3)当2m2-3m-2=-(m2-3m+2),即m=0或m=2时,z为复平面内第二、四象限角平分线上的点对应的复数.(4分)
考点:复数的基本概念.


科目:高中数学 来源:2015届吉林省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
把正整数按一定的规则排成了如图所示的三角形数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左往右数第
行,从左往右数第 个数,若
个数,若 ,则
,则 与
与 的和为( )
的和为( )

A.105 B.103 C.82 D.81
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:解答题
(本小题满分12分)已知椭圆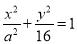 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过 的椭圆的右焦点
的椭圆的右焦点 任作一条斜率为
任作一条斜率为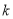 (
( )的直线交椭圆于A,B两点,问在
)的直线交椭圆于A,B两点,问在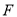 右侧是否存在一点D
右侧是否存在一点D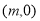 ,连AD、BD分别交直线
,连AD、BD分别交直线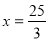 于M,N两点,且以MN为直径的圆恰好过
于M,N两点,且以MN为直径的圆恰好过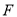 ,若存在,求
,若存在,求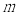 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高一上学期第一次月考数学试卷(解析版) 题型:选择题
集合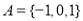 的子集中,含有元素
的子集中,含有元素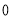 的子集共有( )
的子集共有( )
A.2个 B.4个 C.6个 D.8个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com