
(本小题满分12分)已知椭圆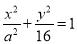 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过 的椭圆的右焦点
的椭圆的右焦点 任作一条斜率为
任作一条斜率为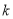 (
( )的直线交椭圆于A,B两点,问在
)的直线交椭圆于A,B两点,问在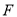 右侧是否存在一点D
右侧是否存在一点D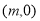 ,连AD、BD分别交直线
,连AD、BD分别交直线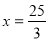 于M,N两点,且以MN为直径的圆恰好过
于M,N两点,且以MN为直径的圆恰好过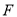 ,若存在,求
,若存在,求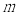 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ)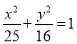 或
或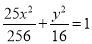 ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)根据椭圆的定义及其 间的基本关系易求得“
间的基本关系易求得“ ”值(不一定是定义中的
”值(不一定是定义中的 ),从而得到椭圆的方程,求解时注意分焦点在
),从而得到椭圆的方程,求解时注意分焦点在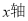 和
和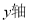 上两种情况进行讨论;(Ⅱ)本题属于解析几何的综合性题型,解题的关键在于将“形”的特征用“数”的形式定量地刻画出来,由与点
上两种情况进行讨论;(Ⅱ)本题属于解析几何的综合性题型,解题的关键在于将“形”的特征用“数”的形式定量地刻画出来,由与点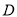 有直接关系的
有直接关系的 四点着手,通过共线关系找到彼此的内在联系和数量关系;其次通过直径所对圆周角是直角来构造向量垂直也是解决本题的一个关键所在,是对已知条件的深层次的挖掘;在些基础上,充分运用方程思想和精确的运算及推理不难得出所求.
四点着手,通过共线关系找到彼此的内在联系和数量关系;其次通过直径所对圆周角是直角来构造向量垂直也是解决本题的一个关键所在,是对已知条件的深层次的挖掘;在些基础上,充分运用方程思想和精确的运算及推理不难得出所求.
试题解析:(Ⅰ)当焦点在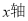 上时,
上时,
由 ,故所求椭圆方程为
,故所求椭圆方程为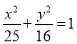 .
.
当焦点在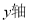 上时,
上时,
由 ,故所求椭圆方程为
,故所求椭圆方程为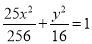 .
.
综上所述,所求椭圆方程为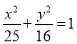 或
或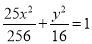 .
.
(Ⅱ)如图所示:
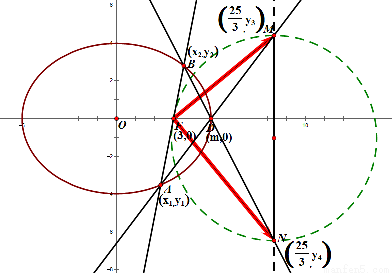
设直线 的方程为
的方程为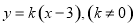 ,
, ,则由
,则由
 ,根据韦达定理(根与系数的关系)得:
,根据韦达定理(根与系数的关系)得:
 ,
, ,
,
 由
由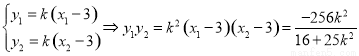 …… ①
…… ①
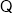
 三点共线,即
三点共线,即 ,且
,且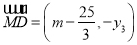 ,
,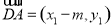 ,
,

 ,同理可得
,同理可得 ,
,

 ……②
……②
根所题意, (直径所对圆周角),即
(直径所对圆周角),即 ,
,

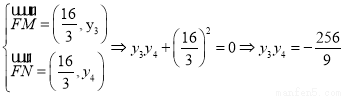 ……③
……③
由①、②、③得: ,
,

 ,
, 由
由 ,
,
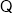 点
点 在
在 的右侧,
的右侧,
 ,
, .
.
 存在满足条件的
存在满足条件的 点,且
点,且 .
.
考点:①椭圆的方程和性质;②直线方程;③向量共线和垂直的动用;④根下系数的关系;⑤数形结合思想;⑥方程思想;⑦推理和运算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届吉林省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知复数z=(2+i)m2--2(1-i).当实数m取什么值时,复数z是:
(1)虚数;(2)纯虚数;(3)复平面内第二、四象限角平分线上的点对应的复数?
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省大连市高一上学期期中考试数学试卷(解析版) 题型:选择题
设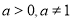 ,函数
,函数 在
在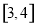 上是增函数,则实数
上是增函数,则实数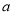 的取值范围是
的取值范围是
(A)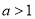
(B)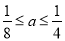 或
或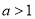
(C)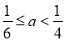 或
或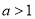
(D)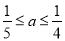 或
或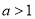
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:解答题
(本小题满分10分)设有两个命题: 关于x的不等式x2+2ax+4>0对一切x∈R恒成立;
关于x的不等式x2+2ax+4>0对一切x∈R恒成立; 函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数.若命题
函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数.若命题 为真,
为真, 为假,则实数a的取值范围是多少?
为假,则实数a的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:选择题
设等差数列{ }{
}{  }的前n 项和为
}的前n 项和为 ,
, ,若
,若  ,则
,则  =
=
A.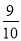 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一阶段考试理科数学试卷(解析版) 题型:解答题
根据下面的要求,求 值.
值.
(Ⅰ)请完成执行该问题的程序框图;
(Ⅱ)以下是解决该问题的程序,请完成执行该问题的程序.
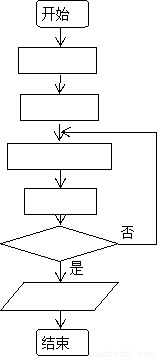
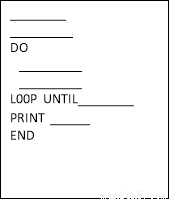
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com