
分析 (1)根据二次函数的性质得到判别式△=0,求出b2=4c,代入b2+c2+2,求出其范围即可;
(22)二次函数f(x)=x2+bx+c(b≥0,c∈R)的对称轴是x=-$\frac{b}{2}$,定义域为[-1,0],按照对称轴在定义域[-1,0]内、在[-1,0]的左边和在[-1,0]的右边三种情况分别求函数的值域,令其和题目条件中给出的值域相等,求b和c.
解答 解:(1)由于f(x)的图象与x轴有且仅有一个交点,故△=0,
即△=b2-4c=0⇒b2=4c,
则b2+c2+2=c2+4c+2=(c+2)2-4≥-4;
(2)解:设符合条件的f(x)存在,
∵函数图象的对称轴是x=-$\frac{b}{2}$,
又b≥0,∴-$\frac{b}{2}$≤0.
①当-$\frac{1}{2}$<-$\frac{b}{2}$≤0,即0≤b<1时,
函数x=-$\frac{b}{2}$有最小值-1,则 $\left\{\begin{array}{l}{f(-\frac{b}{2})=-1}\\{f(-1)=0}\end{array}\right.$⇒$\left\{\begin{array}{l}{\frac{{b}^{2}}{4}-\frac{{b}^{2}}{2}+c=1}\\{1-b+c=0}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=0}\\{c=-1}\end{array}\right.$或 $\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$(舍去).
②当-1<-$\frac{b}{2}$≤-$\frac{1}{2}$,即1≤b<2时,则 $\left\{\begin{array}{l}{f(-\frac{b}{2})=-1}\\{f(0)=0}\end{array}\right.$⇒$\left\{\begin{array}{l}{b=2}\\{c=0}\end{array}\right.$(舍去)或 $\left\{\begin{array}{l}{b=-2}\\{c=0}\end{array}\right.$(舍去).
③当-$\frac{b}{2}$≤-1,即b≥2时,函数在[-1,0]上单调递增,则 $\left\{\begin{array}{l}{f(-1)=-1}\\{f(0)=0}\end{array}\right.$,解得 $\left\{\begin{array}{l}{b=2}\\{c=0}\end{array}\right.$,
综上所述,符合条件的函数有两个,
f(x)=x2-1或f(x)=x2+2x.
点评 本题考查二次函数在特定区间上的值域问题,及分类讨论思想,难度一般.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
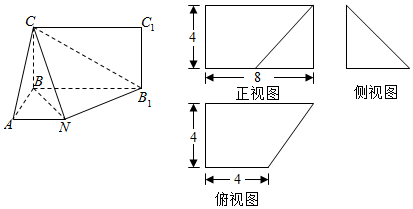
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
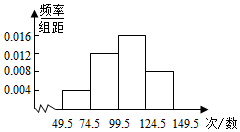 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右前三个小组的频率分别为 0.1,0.3,0.4,第一小组的频数为 5.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右前三个小组的频率分别为 0.1,0.3,0.4,第一小组的频数为 5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=sin($\frac{1}{2}$x+$\frac{π}{4}$) | C. | y=sin$\frac{1}{2}$x | D. | y=sin($\frac{1}{2}$x+$\frac{π}{12}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com