练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，弧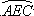是半径为a的半圆，AC为直径，点E为弧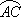的中点，点B和点C为线段AD的三等分点．平面AEC外一点F满足FB＝DF＝a，．

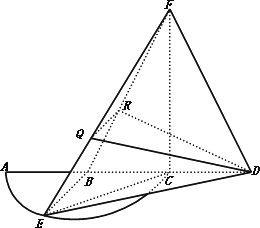
    (1)证明：FC⊥平面AEC；

    (2)证明：EB⊥FD；

    (3)已知点Q，R分别为线段FE，FB上的点，使得，求平面BED与平面RQD所成二面角的正弦值．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，弧AEC是半径为a的半圆，AC为直径，点E为弧AC的中点，点B和点C为线段AD的三等分点，平面AEC外一点F满足FC⊥平面BDE，FB=
    		5
    a    ．
    （1）证明：平面BEF⊥平面BDF；
    （2）求二面角F-DE-B的正切值．

    查看答案和解析>>

    科目：高中数学 来源：2009年合肥市高三第一次教学质量检测数学(理科)试题 题型：044

    如图，O是半径为2的球的球心，点A．B．C在球面上，OA．OB．OC两两垂直，E．F分别是大圆的弧AB与AC的中点．

    (1)求证：EF∥面OBC；

    (2)求多面体OAEBCF的体积；

    (3)建立适当的空间直角坐标系，求的坐标，并求异面直线OF和CE的夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源：2009年合肥市高三第一次教学质量检测数学(文科)试题 题型：044

    如图，O是半径为2的球的球心，点A．B．C在球面上，OA．OB．OC两两垂直，E．F分别是大圆的弧AB与AC的中点．

    (1)求证：EF∥面OBC；

    (2)求多面体OAEBCF的体积；

    (3)建立适当的空间直角坐标系，求的坐标，并求异面直线OF和CE的夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （12分）如图，O 是半径为2的球的球心，点A．B．C在球面上，OA．OB．OC两两垂直，E．F分别是大圆的弧AB与AC的中点。

    （1）       求证：EF//面OBC；

    （2）       求多面体OAEBCF的体积；

    （3）       建立适当的空间直角坐标系，求的坐标，

    并求异面直线OF和CE的夹角的余弦值。

    查看答案和解析>>

    同步练习册答案