Question

3．已知函数$f（x）=\left\{{\begin{array}{l}{1-|x|，x＜1}\\{{{（x-1）}^2}，x＞1}\end{array}}\right.$，若方程f²（x）+af（x）+b=0有五个不同的根，则a的取值范围为（-2，-1）．

Answer 1

分析 设t=f（x），作出函数f（x）的图象，根据数形结合以及方程根的关系进行判断求解即可．

解答 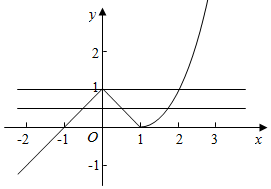解：设t=f（x），
作出函数f（x）的图象如图
则当t=1时，t=f（x）有两个根，
当t＞1或t≤0时，t=f（x）有一个根，
当0＜t＜1时，t=f（x）有3个根，
若方程f²（x）+af（x）+b=0有五个不同的根，
则等价为方程t²+at+b=0有两个不同的根，t₁=1或0＜t₂＜1，
则1＜t₁+t₂＜2，
即1＜-a＜2，则-2＜a＜-1，
即a的取值范围为（-2，-1），
故答案为：（-2，-1）．

点评 本题主要考查函数与方程的应用，利用换元法结合数形结合以及函数图象的关系建立不等式关系是解决本题的关键．