
【题目】已知函数f(x)=ax2+bx+c(a,b,c∈R,a≠0),对任意的x∈R,都有f(x﹣4)=f(2﹣x)成立,
(1)求2a﹣b的值;
(2)函数f(x)取得最小值0,且对任意x∈R,不等式x≤f(x)≤( ![]() )2恒成立,求函数f(x)的解析式;
)2恒成立,求函数f(x)的解析式;
(3)若方程f(x)=x没有实数根,判断方程f(f(x))=x根的情况,并说明理由.
【答案】
(1)解:由f(x﹣4)=f(2﹣x)成立,可得函数y=f(x)图象的对称轴方程为x= ![]() =﹣1,
=﹣1,
∴﹣ ![]() =﹣1,∴2a﹣b=0
=﹣1,∴2a﹣b=0
(2)解:当x=﹣1 时,f(x)=a﹣b+c=0,
对于不等式x≤f(x)≤( ![]() )2 ,当x=1时,有1≤f(1)≤1,∴f(1)=a+b+c=1.
)2 ,当x=1时,有1≤f(1)≤1,∴f(1)=a+b+c=1.
由以上方程解得 a= ![]() =c,b=
=c,b= ![]() ,∴函数的解析式为
,∴函数的解析式为 ![]()
(3)解:因为方程f(x)=x无实根,所以当a>0时,不等式f(x)>x恒成立,
∴f(f(x))>f(x)>x,故方程f(f(x))=x无实数解.
当a<0时,不等式f(x)<x恒成立,∴f(f(x))<f(x)<x,
故方程f(f(x))=x无实数解,
综上得:方程f(f(x))=x无实数解
【解析】(1)由f(x﹣4)=f(2﹣x)成立,可得函数y=f(x)图象的对称轴方程为 x=﹣ ![]() =﹣1,由此求得 2a﹣b的值. (2)当x=﹣1 时,f(x)=a﹣b+c=0,对于不等式x≤f(x)≤(
=﹣1,由此求得 2a﹣b的值. (2)当x=﹣1 时,f(x)=a﹣b+c=0,对于不等式x≤f(x)≤( ![]() )2 , 当x=1时,由1≤f(1)≤1,可得f(1)=a+b+c=1.求得a、b、c的值,可得函数的解析式.(3)由题意可得,当a>0时,不等式f(x)>x恒成立,f(f(x))>f(x)>x,方程f(f(x))=x无实数解.当a<0时,由不等式f(x)<x恒成立,可得f(f(x))<f(x)<x,方程f(f(x))=x无实数解,综合可得结论.
)2 , 当x=1时,由1≤f(1)≤1,可得f(1)=a+b+c=1.求得a、b、c的值,可得函数的解析式.(3)由题意可得,当a>0时,不等式f(x)>x恒成立,f(f(x))>f(x)>x,方程f(f(x))=x无实数解.当a<0时,由不等式f(x)<x恒成立,可得f(f(x))<f(x)<x,方程f(f(x))=x无实数解,综合可得结论.
【考点精析】关于本题考查的二次函数的性质,需要了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能得出正确答案.
上递减才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=﹣x2+(3﹣2m)x+2+m(0<m≤1).
(1)若x∈[0,m],证明:f(x)≤ ![]() ;
;
(2)求|f(x)|在[﹣1,1]上的最大值g(m).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的参数方程;
的参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,试求
上动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩(成绩为整数,满分为100),其中一个数字被污损,则乙的平均成绩不低于甲的平均成绩的概率为( ) 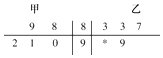
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批土鸡蛋中,随机抽取n个得到一个样本,其重量(单位:克)的频数分布表如表:
分组(重量) | [80,85) | [85,90) | [90,95) | [95,100] |
频数(个) | 10 | 50 | m | 15 |
已知从n个土鸡蛋中随机抽取一个,抽到重量在在[90,95)的土鸡蛋的根底为 ![]()
(1)求出n,m的值及该样本的众数;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的土鸡蛋中共抽取5个,再从这5个土鸡蛋中任取2 个,其重量分别是g1 , g2 , 求|g1﹣g2|≥10概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行六面体ABCD﹣A1B1C1D1中,侧棱B1B长为3,底面是边长为2的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,则AE+C1E的最小值为( )
A.![]()
B.5
C.2![]()
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥的侧棱![]() 底面
底面![]() ,且底面
,且底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在侧棱上.
在侧棱上.
(1)求证:![]() 平面
平面![]() ;
;
(2)若侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com