
【题目】某折叠餐桌的使用步骤如图所示,有如图检查项目:
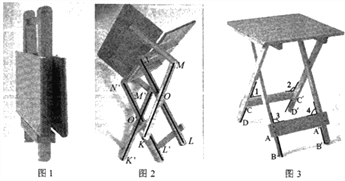
项目①:折叠状态下(如图1),检查四条桌腿长相等;
项目②:打开过程中(如图2),检查![]() ;
;
项目③:打开过程中(如图2),检查![]() ;
;
项目④:打开后(如图3),检查![]() ;
;
项目⑤:打开后(如图3),检查![]() .
.
在检查项目的组合中,可以正确判断“桌子打开之后桌面与地面平行的是”( )
A. ①②③ B. ②③④ C. ②④⑤ D. ③④⑤
【答案】B
【解析】A项, 项目②和项目③可推出项目①,所以判断项目②和项目③,若![]() ,则
,则![]() 较低,
较低, ![]() 较高,所以不平行,错误;B项,
较高,所以不平行,错误;B项, ![]() 面
面![]() 面
面![]() ,
,![]() 平行底面,
平行底面, ![]() 面
面![]() ,所以桌面平行于底面,故正确;C项,由图3的正视图可得,
,所以桌面平行于底面,故正确;C项,由图3的正视图可得, ![]() ,但
,但![]() 与
与![]() 是否相等不确定,所以不确定
是否相等不确定,所以不确定![]() 与
与![]() 是否平行,又因为
是否平行,又因为![]() ,所以不确定
,所以不确定![]() 与
与![]() 是否平行,故错误;D项,
是否平行,故错误;D项, ![]() ,但不确定
,但不确定![]() 与
与![]() 的关系,所以无法判断
的关系,所以无法判断![]() 与底面的关系,错误;综上所述,应选B.
与底面的关系,错误;综上所述,应选B.
点睛:本题考查空间点、线、面的位置关系以及线面平行和面面平行的判断,需要学生结合所学知识与实际应用相联系,并结合选项判断,属于难题. 其中线线平行、面面平行有传递性,而线面平行没有传递性,如a∥α,a∥β不一定得到α∥β, 同时a∥α,b∥α也不一定得到a∥b.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的焦距为
(a>b>0)的焦距为![]() ,且椭圆C过点A(1,
,且椭圆C过点A(1, ![]() ),
),
(Ⅰ)求椭圆C的方程;
(Ⅱ)若O是坐标原点,不经过原点的直线L:y=kx+m与椭圆交于两不同点P(x1,y1),Q(x2,y2),且y1y2=k2x1x2,求直线L的斜率k;
(Ⅲ)在(Ⅱ)的条件下,求△OPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn=n(3﹣bn),求数列{cn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1= ![]() an+t,a1=
an+t,a1= ![]() (t为常数,且t≠
(t为常数,且t≠ ![]() ).
).
(1)证明:{an﹣2t}为等比数列;
(2)当t=﹣ ![]() 时,求数列{an}的前几项和最大?
时,求数列{an}的前几项和最大?
(3)当t=0时,设cn=4an+1,数列{cn}的前n项和为Tn , 若不等式 ![]() ≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知含有![]() 个元素的正整数集
个元素的正整数集![]() (
(![]() ,
, ![]() )具有性质
)具有性质![]() :对任意不大于
:对任意不大于![]() (其中
(其中![]() )的正整数
)的正整数![]() ,存在数集
,存在数集![]() 的一个子集,使得该子集所有元素的和等于
的一个子集,使得该子集所有元素的和等于![]() .
.
(Ⅰ)写出![]() ,
, ![]() 的值;
的值;
(Ⅱ)证明:“![]() ,
, ![]() ,…,
,…, ![]() 成等差数列”的充要条件是“
成等差数列”的充要条件是“![]() ”;
”;
(Ⅲ)若![]() ,求当
,求当![]() 取最小值时
取最小值时![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(14分)一根直木棍长为6m,现将其锯为2段.
(1)若两段木棍的长度均为正整数,求恰有一段长度为2m的概率;
(2)求锯成的两段木棍的长度均大于2m的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com