
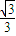 的概率为 .
的概率为 .  同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源: 题型:
 如图所示,在边长为4的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将△ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.
如图所示,在边长为4的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将△ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.查看答案和解析>>
科目:高中数学 来源:2013届度黑龙江大庆实验中学高二上学期期末考试文科数学试卷 题型:选择题
一只蚂蚁在边长为4的正三角形内爬行,某时刻此蚂蚁距三角形三个顶点的距离均超过1的概率为( )
A. B.
B.  C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com