

 的值;
的值; 成立的x的取值集合.
成立的x的取值集合.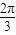 代入f(x)解析式,利用两角和与差的余弦函数公式及特殊角的三角函数值化简即可得到结果;
代入f(x)解析式,利用两角和与差的余弦函数公式及特殊角的三角函数值化简即可得到结果;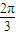 )=cos
)=cos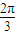 cos(
cos(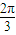 -
-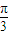 )=cos
)=cos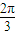 cos
cos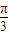 =-cos2
=-cos2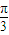 =-
=- ;
;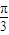 )=cosx(
)=cosx( cosx+
cosx+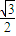 sinx)
sinx) cos2x+
cos2x+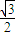 sinxcosx=
sinxcosx= (1+cos2x)+
(1+cos2x)+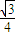 sin2x=
sin2x= cos(2x-
cos(2x-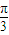 )+
)+ ,
, ,化为
,化为 cos(2x-
cos(2x-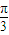 )+
)+ <
< ,即cos(2x-
,即cos(2x-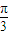 )<0,
)<0,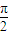 <2x-
<2x-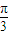 <2kπ+
<2kπ+ (k∈Z),
(k∈Z),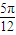 <x<kπ+
<x<kπ+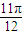 (k∈Z),
(k∈Z), 成立的x取值集合为{x|kπ+
成立的x取值集合为{x|kπ+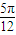 ,kπ+
,kπ+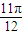 (k∈Z)}.
(k∈Z)}.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:2010年浙江省温州市苍南县龙港高中高考数学仿真模拟试卷(文科)(解析版) 题型:解答题

 的值;
的值; 对称,且t∈(0,π),求t的值.
对称,且t∈(0,π),求t的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com