解:设椭圆的方程为
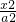
+
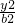
=1(a>b>0),F
1(-c,0)、F
2(c,0).
因为点P在椭圆上,所以|PF
1|+|PF
2|=2a.…(2分)
在△PF
1F
2中,由余弦定理,得
|F
1F
2|
2=|PF
1|
2+|PF
2|
2-2|PF
1|•|PF
2|cos

=(|PF
1|+|PF
2|)
2-3|PF
1|•|PF
2|,
即4c
2=4a
2-3|PF
1|•|PF
2|.…(6分)
又因S
△PF1F2=3

,所以

|PF
1|•|PF
2|sin

=3

,得|PF
1|•|PF
2|=12.
所以4c
2=4a
2-36,又e=

=

,
故a
2=25,c
2=16,b
2=9,
∴所求椭圆的方程为
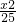
+
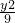
=1.…(12分)
分析:根据点P是椭圆的左支上的一点,及双曲线的定义可知|PF
2|+|PF
1|=2a,由,∠F
1PF
2=

,且△PF
1F
2的面积为3

,可以求得|PF
2|•|PF
1|的值,根据余弦定理可以求得a,c的一个方程,双曲线的离心率为2,根据双曲线的离心率的定义式,可以求得a,c的一个方程,解方程组即可求得该椭圆的方程.
点评:此题是个中档题.考查椭圆的定义和待定系数法求椭圆的标准方程,及利用余弦定理解圆锥曲线的焦点三角形,解题过程注意整体代换的方法,简化计算.

 ,F1、F2分别为椭圆的左、右焦点,椭圆上有一点P,∠F1PF2=
,F1、F2分别为椭圆的左、右焦点,椭圆上有一点P,∠F1PF2= ,且△PF1F2的面积为3
,且△PF1F2的面积为3 ,求椭圆的方程.
,求椭圆的方程.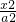 +
+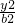 =1(a>b>0),F1(-c,0)、F2(c,0).
=1(a>b>0),F1(-c,0)、F2(c,0). =(|PF1|+|PF2|)2-3|PF1|•|PF2|,
=(|PF1|+|PF2|)2-3|PF1|•|PF2|, ,所以
,所以 |PF1|•|PF2|sin
|PF1|•|PF2|sin =3
=3 ,得|PF1|•|PF2|=12.
,得|PF1|•|PF2|=12. =
= ,
,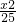 +
+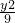 =1.…(12分)
=1.…(12分) ,且△PF1F2的面积为3
,且△PF1F2的面积为3 ,可以求得|PF2|•|PF1|的值,根据余弦定理可以求得a,c的一个方程,双曲线的离心率为2,根据双曲线的离心率的定义式,可以求得a,c的一个方程,解方程组即可求得该椭圆的方程.
,可以求得|PF2|•|PF1|的值,根据余弦定理可以求得a,c的一个方程,双曲线的离心率为2,根据双曲线的离心率的定义式,可以求得a,c的一个方程,解方程组即可求得该椭圆的方程.

 阅读快车系列答案
阅读快车系列答案 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.