
分析 (1)利用矩阵的乘法,可求实数a的值,根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
(2)由特征值、特征向量定义可知,Aα1=λ1α1,由此可建立方程组,从而可求矩阵A.
解答 解:(1)由$(\begin{array}{l}{2}&{a}\\{2}&{1}\end{array})$$[\begin{array}{l}{1}\\{-2}\end{array}]$=$[\begin{array}{l}{-4}\\{0}\end{array}]$,∴2-2a=-4,∴a=3;
∴M=$[\begin{array}{l}{2}&{3}\\{2}&{1}\end{array}]$,则矩阵M的特征多项式为f(λ)=(λ+1)(λ-4),
令f(λ)=0,可求得特征值为λ1=-1,λ2=4,
设λ1=-1对应的一个特征向量为α=$[\begin{array}{l}{x}\\{y}\end{array}]$
则由λ1α=Mα,得x+y=0,可令x=1,则y=-1,
∴矩阵M的一个特征值λ1=-1对应的一个特征向量为$[\begin{array}{l}{1}\\{-1}\end{array}]$,
同理可得矩阵M的一个特征值λ2=4对应的一个特征向量为$[\begin{array}{l}{3}\\{2}\end{array}]$.
(2)由特征值、特征向量定义可知,Aα1=λ1α1,
即$(\begin{array}{l}{a}&{b}\\{c}&{d}\end{array})$$(\begin{array}{l}{1}\\{-1}\end{array})$=-1×$(\begin{array}{l}{1}\\{-1}\end{array})$,得$\left\{\begin{array}{l}{a-b=-1}\\{c-d=1}\end{array}\right.$
同理可得$\left\{\begin{array}{l}{3a+2b=12}\\{3c+2d=8}\end{array}\right.$,解得a=2,b=3,c=2,d=1.
因此矩阵A=$[\begin{array}{l}{2}&{3}\\{2}&{1}\end{array}]$.
点评 本小题主要考查矩阵与变换、矩阵的特征值与特征向量等基础知识,考查运算求解能力.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
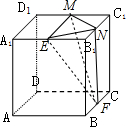 如图,在正方体ABCD-A1B1C1D1中,E,F,M,N分别是A1B1,BC,C1D1和B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E,F,M,N分别是A1B1,BC,C1D1和B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com