
设函数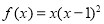 ,
,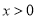 .
.
(1)求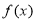 的极值;
的极值;
(2)设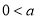 ≤
≤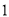 ,记
,记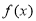 在
在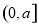 上的最大值为
上的最大值为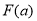 ,求函数
,求函数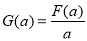 的最小值;
的最小值;
(3)设函数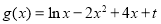 (
(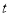 为常数),若使
为常数),若使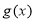 ≤
≤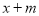 ≤
≤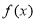 在
在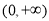 上恒成立的实数
上恒成立的实数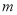 有且只有一个,求实数
有且只有一个,求实数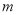 和
和 的值.
的值.
科目:高中数学 来源:2017届湖北省沙市高三上学期第二次考试理科数学卷(解析版) 题型:选择题
某物流公司为了配合“北改”项目顺利进行,决定把三环内的租用仓库搬迁到北三环外重新租地建设。已知仓库每月占用费y1与仓库到车站的距离成反比,而每月车载货物的运费y2与仓库到车站的距离成正比。据测算,如果在距离车站10千米处建仓库,这两项费用y1,y2分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
A.5千米处 B.4千米处 C.3千米处 D.2千米处
查看答案和解析>>
科目:高中数学 来源:2017届广东省高三9月月考数学(文)试卷(解析版) 题型:
已知椭圆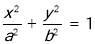
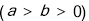 的离心率
的离心率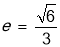 ,过点
,过点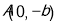 和
和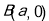 的直线与原点的距离为
的直线与原点的距离为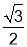 .
.
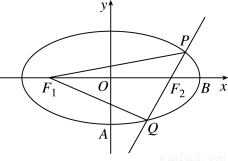
(1)求椭圆的方程;
(2)设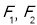 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过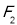 作直线交椭圆于
作直线交椭圆于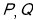 两点,求△
两点,求△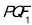 的内切圆半径
的内切圆半径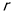 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com