
【题目】若正实数a,b满足a+b=1,则( )
A.![]() 有最大值4
有最大值4
B.ab有最小值 ![]()
C.![]() 有最大值
有最大值 ![]()
D.a2+b2有最小值 ![]()
【答案】C
【解析】解:∵正实数a,b满足a+b=1, ∴ ![]() =
= ![]() =2+
=2+ ![]() ≥2+2=4,故
≥2+2=4,故 ![]() 有最小值4,故A不正确.
有最小值4,故A不正确.
由基本不等式可得 a+b=1≥2 ![]() ,∴ab≤
,∴ab≤ ![]() ,故ab有最大值
,故ab有最大值 ![]() ,故B不正确.
,故B不正确.
由于 ![]() =a+b+2
=a+b+2 ![]() =1+2
=1+2 ![]() ≤2,∴
≤2,∴ ![]() ≤
≤ ![]() ,故
,故 ![]() 有最大值为
有最大值为 ![]() ,故C正确.
,故C正确.
∵a2+b2 =(a+b)2﹣2ab=1﹣2ab≥1﹣ ![]() =
= ![]() ,故a2+b2有最小值
,故a2+b2有最小值 ![]() ,故D不正确.
,故D不正确.
故选:C.
由于 ![]() =
= ![]() =2+
=2+ ![]() ≥4,故A不正确.
≥4,故A不正确.
由基本不等式可得 a+b=1≥2 ![]() ,可得 ab≤
,可得 ab≤ ![]() ,故B不正确.
,故B不正确.
由于 ![]() =1+2
=1+2 ![]() ≤2,故
≤2,故 ![]() ≤
≤ ![]() ,故 C 正确.
,故 C 正确.
由a2+b2 =(a+b)2﹣2ab≥1﹣ ![]() =
= ![]() ,故D不正确.
,故D不正确.


科目:高中数学 来源: 题型:
【题目】过点P(3,2)且在两坐标轴上的截距相等的直线方程是( )
A.x﹣y﹣1=0
B.x+y﹣5=0或2x﹣3y=0
C.x+y﹣5=0
D.x﹣y﹣1=0或2x﹣3y=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6. 
(Ⅰ)估计所抽取的数学成绩的众数;
(Ⅱ)用分层抽样的方法在成绩为[80,90)和[90,100]这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在[90,100]恰有1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18﹣ ![]() ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2= ![]() (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出人. 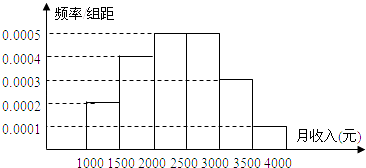
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(1)当x∈[0, ![]() ]时,求f(x)的值域;
]时,求f(x)的值域;
(2)用五点法在图中作出y=f(x)在闭区间[﹣ ![]() ,
, ![]() ]上的简图;
]上的简图;
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变化得到? 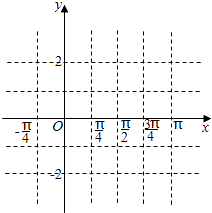
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( ) 
A.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
B.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
C.若方程f(x)=m在[﹣ ![]() ,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣
,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣ ![]() ]
]
D.将函数f(x)的图象向左平移 ![]() 个单位可得到一个偶函数
个单位可得到一个偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 1=a1≤a2≤…≤a7 , 其中a1 , a3 , a5 , a7 成公比为q的等比数列,a2 , a4 , a6成公差为1的等差数列,则q的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA,PB,切点为A,B.
(1)当切线PA的长度为 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P在直线l上运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段AB长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com