
如图,侧棱垂直底面的三棱柱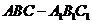 中,
中,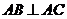 ,
,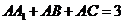 ,
,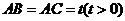 ,
,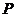 是侧棱
是侧棱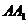 上的动点.
上的动点.

(Ⅰ)当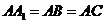 时,求证:
时,求证: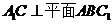 ;
;
(Ⅱ)试求三棱锥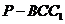 的体积
的体积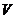 取得最大值时的
取得最大值时的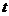 值;
值;
(Ⅲ)若二面角 的平面角的余弦值为
的平面角的余弦值为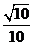 ,试求实数
,试求实数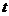 的值.
的值.
本小题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想及应用意识. 满分13分.
解:(Ⅰ)证法一:∵ 面
面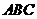 ,∴
,∴ ,
, .
.
又∵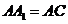 ,∴四边形
,∴四边形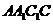 是正方形,
是正方形,
∴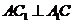 .
………1分
.
………1分
∵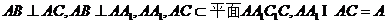 ,
,
∴ .
………2分
.
………2分
又∵ ,
∴
,
∴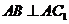 .
………3分
.
………3分
∵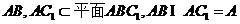 ,
,
∴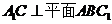 .
………4分
.
………4分
证法二:∵ 面
面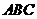 ,∴
,∴ ,
, .
.
又∵ ,
,
∴分别以 所在直线为
所在直线为 轴建立空间直角坐标系. ……1分
轴建立空间直角坐标系. ……1分
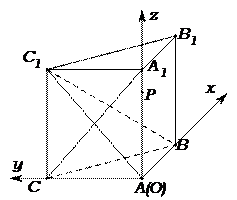 则
则 ,
,
 ,
,
∴ , …2分
, …2分
∴ .
…3分
.
…3分
又∵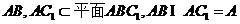
∴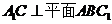 .
…4分
.
…4分
证法三:∵ 面
面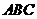 ,∴
,∴ ,
, .
.
又∵ ,
,
∴分别以 所在直线为
所在直线为 轴建立空间直角坐标系. ……1分
轴建立空间直角坐标系. ……1分
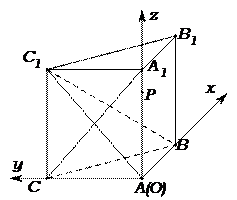 则
则 ,
,
 .
.
设平面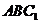 的法向量
的法向量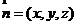 ,
,
则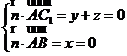 ,解得
,解得 .
.
令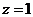 ,则
,则 , ……3分
, ……3分
∵ ,
∴
,
∴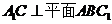 .
……4分
.
……4分
(Ⅱ)∵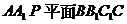 ,
,
∴点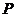 到平面
到平面 的距离等于点
的距离等于点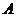 到平面
到平面 的距离
的距离
∴ ,
…5分
,
…5分
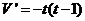 ,
,
令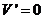 ,得
,得 (舍去)或
(舍去)或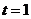 ,
,
列表,得
|
|
|
1 |
|
|
|
+ |
0 |
- |
|
|
递增 |
极大值 |
递减 |
∴当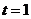 时,
时,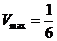 .
…8分
.
…8分
(Ⅲ)分别以 所在直线为
所在直线为 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则 ,
,
 ,
,
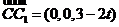 ,
,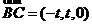 . ……9分
. ……9分
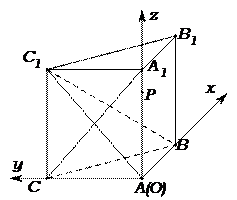 设平面
设平面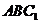 的法向量
的法向量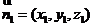 ,
,
则 ,解得
,解得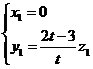 ,
,
令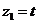 ,则
,则 .
…10分
.
…10分
设平面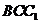 的法向量
的法向量 ,
,
则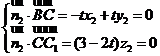 .
.
由于 ,所以解得
,所以解得 .
.
令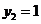 ,则
,则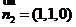 .
…11分
.
…11分
设二面角 的平面角为
的平面角为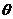 ,
,
则有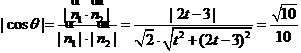 .
.
化简得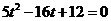 ,解得
,解得 (舍去)或
(舍去)或 .
.
所以当 时,二面角
时,二面角 的平面角的余弦值为
的平面角的余弦值为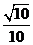 . …13分
. …13分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
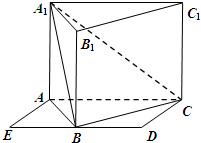 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.查看答案和解析>>
科目:高中数学 来源: 题型:
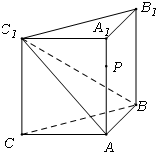 如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
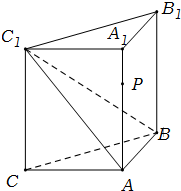 (2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
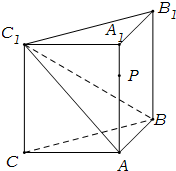 (2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
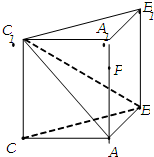 (2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).
(2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).
| ||
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com