
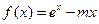
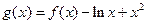 存在两个零点,求m的取值范围;
存在两个零点,求m的取值范围;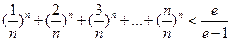 。
。科目:高中数学 来源:不详 题型:解答题
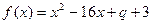 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
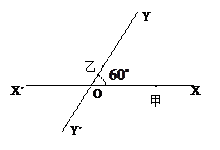
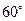 的直路
的直路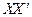 ,
,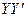 ,交点是
,交点是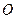 ,甲、乙分别在
,甲、乙分别在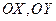 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿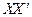 方向用2 km/h的速度,乙沿
方向用2 km/h的速度,乙沿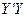 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在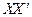 上点A处,乙在
上点A处,乙在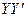 上点B处.
上点B处.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
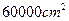 ,四周空白的宽度为
,四周空白的宽度为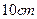 ,栏与栏之间的中缝空白的宽度为
,栏与栏之间的中缝空白的宽度为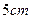 ,怎样确定广告矩形栏目高与宽的尺寸(单位:
,怎样确定广告矩形栏目高与宽的尺寸(单位: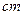 ),能使整个矩形广告面积最小.
),能使整个矩形广告面积最小.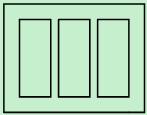
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
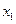 ,
,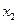 ,……
,……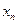 中的最大数为max
中的最大数为max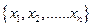 ,最小数为min
,最小数为min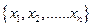 。已知ABC的三边长位a,b,c(
。已知ABC的三边长位a,b,c(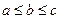 ),定义它的亲倾斜度为
),定义它的亲倾斜度为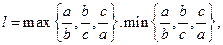
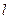 =1”是“
=1”是“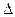 ABC为等边三角形”的
ABC为等边三角形”的| A.必要而不充分的条件 |
| B.充分而不必要的条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com