
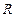 上的偶函数
上的偶函数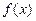 满足
满足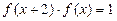 对于
对于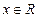 恒成立,且
恒成立,且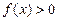 ,则
,则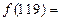 ________
________科目:高中数学 来源:不详 题型:解答题
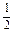 x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?
x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
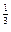 ,h(x)=logax,a满足loga(1-a2)>0,那么当x>1时必有 ( )
,h(x)=logax,a满足loga(1-a2)>0,那么当x>1时必有 ( )| A.h(x)<g(x)<f(x) | B.h(x)<f(x)<g(x) |
| C.f(x)<g(x)<h(x) | D.f(x)<h(x)<g(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com