练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知U={x|x取不大于30的质数}，A、B是U的两个子集，

    且A∩(B)={5,13,23},(A)∩B={11,19,29},(A)∩(B)={3,7},

    求A、B.

    解：如图可得A={2，5，13，17，23},B={2，11，17，19，29}.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知全集U={x|x取不大于20的质数}，A、B是U的两个子集，且A∩（?UB）={3，5}，（?UA）∩B={7，19}，（?UA）∩（?UB）={2，17}，则集合A=
    {3，5，11，13}，
    {3，5，11，13}，
    ，B=
    {7，11，13，19}
    {7，11，13，19}
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数.

    （Ⅰ）若函数f(x)在区间上为增函数，求实数的取值范围；w.w.w.k.s.5.u.c.o.m    

    （Ⅱ）若是函数f(x)的极值点，求函数f(x)在区间上的最大值；

    （Ⅲ）在（Ⅱ）的条件下，是否存在实数b，使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点？若存在，请求出b的取值范围；若不存在，试说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广东省汕头市高二（下）质量监测数学试卷（文科）（解析版） 题型：解答题

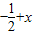    已知函数f（x）=ax2+bx+c（a≠0）满足：①f（0）=0；②?x∈R，f（x）≥x；③f（）=f（）．
    （1）求f（x）的表达式；
    （2）试讨论函数g（x）=f（x）-2x在区间[-2，2]内的单调性；
    （3）是否存在实数t，使得函数h（x）=f（x）-x2-x+t与函数u（x）=|log2x|（x∈（0，2]）的图象恒有两个不同交点，如果存在，求出相应t的取值范围；如果不存在，说明理由．

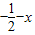    查看答案和解析>>

    科目：高中数学 来源：2011年辽宁省沈阳四校协作体高二上学期期中考试数学 题型：解答题

    本题满分10分）已知全集U＝R，集合A＝{x|x2－x－6<0}，B＝{x|x2＋2x－8>0}，

    C＝{x|x2－4ax＋3a2<0}（a<0），

    （1）；

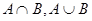    （2）若命题p: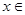∁U(A∪B), 命题q: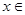C，若p是q的充分不必要条件，求实数a的取值范围．

     

    查看答案和解析>>

    同步练习册答案