
如图,某开发商准备开发一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一游泳池,其余的地方种花。若BC=a,
∠ABC=![]() ,设△ABC的面积为S1,正方形PQRS的面积为S2。
,设△ABC的面积为S1,正方形PQRS的面积为S2。

(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)当a为定值, ![]() 变化时,求
变化时,求![]() 的最大值,并求此时的角
的最大值,并求此时的角![]() 。
。
科目:高中数学 来源: 题型:
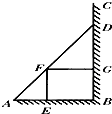 如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2的比值
如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2的比值| S1 | S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
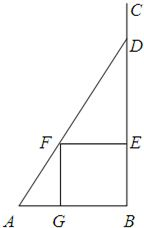 如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2比
如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2比| S1 |
| S2 |
| π |
| 4 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题共3个小题,第1、2小题满分各5分,第3小题满分6分.
本题共3个小题,第1、2小题满分各5分,第3小题满分6分.| S1 |
| S2 |
| atanθ |
| 1+tanθ |
查看答案和解析>>
科目:高中数学 来源:2010-2011年吉林省长春市十一中高一第二学期期中考试理科数学 题型:解答题
..如图,某小区准备在一直角围墙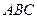 内的空地上植造“绿地
内的空地上植造“绿地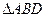 ”,其中
”,其中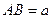 ,
,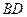 长可根据需要进行调节(
长可根据需要进行调节(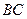 足够长),现规划在
足够长),现规划在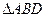 内接正方形
内接正方形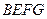 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积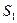 与种花的面积
与种花的面积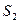 的比
的比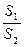 为
为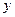 ,
,
(1)设角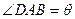 ,将
,将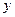 表示成
表示成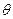 的函数关系;
的函数关系;
(2)当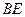 为多长时,
为多长时,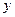 有最小值,最小值是多少?
有最小值,最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com