Question

已知抛物线y²＝2x的焦点是F，点P是抛物线上的动点，又有点A(3,2)．

则|PA|＋|PF|的最小值是       ，取最小值时P点的坐标           ．

 

Answer 1

【答案】

，

【解析】

试题分析：作PM⊥准线l，M为垂足，由抛物线的定义可得|PA|+|PF|=|PA|+|PM|，故当P，A，M三点共线时，|PA|+|PM|最小为|AM|，此时，P点的纵坐标为2，代入抛物线的方程可求得P点的横坐标为1，从而得到P点的坐标．解：由题意可得F（，0）准线方程为 x=-，作PM⊥准线l，M为垂足，由抛物线的定义可得|PA|+|PF|=|PA|+|PM|，故当P，A，M三点共线时，|PA|+|PM|最小为|AM|=3-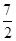（-）=，此时，P点的纵坐标为2，代入抛物线的方程可求得P点的横坐标为2，故P点的坐标为（2，2），

故答案为：，（2，2）．

考点：椭圆定义

点评：本题考查椭圆的定义、标准方程，以及简单性质的应用，判断当P，A，M三点共线时，|PA|+|PM|最小为|AM|，是解题的关键．