
某科技公司生产一种产品的固定成本为20 000元,每生产一个产品增加投资100元,已知总收益满足函数R(x)=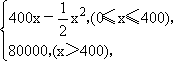 (其中x是产品的月产量),求每月生产多少个产品时该科技公司的利润最大?最大利润是多少?(注:总收益=总成本+利润)
(其中x是产品的月产量),求每月生产多少个产品时该科技公司的利润最大?最大利润是多少?(注:总收益=总成本+利润)
|
答:当每月生产300个产品时,该科技公司获得的利润最大,此时,获得的最大利润为25 000元. 分析:如果每月的产量为x个,根据题意,生产的成本满足函数g(x)=20 000+100x,因此,公司所获得的利润满足函数f(x)=R(x)-g(x). 解:设科技公司的月产量为x个,则总成本为20 000+100x元,所以总利润为 f(x)= 当0≤x≤400时,f(x)= 当x>400时,f(x)<60 000-100×400<25 000. 综上所述,当x=300时,函数f(x)的最大值为25 000. 点评:这是一个分段函数求最值的问题.求解这类问题时应该先分别求出各段上的最值,然后再比较各段上的最值,最终得到函数在定义域上的最值,从而得到符合题意的解. |


科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| t2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省合肥32中高三(上)9月月考数学试卷(文科)(解析版) 题型:解答题
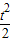 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com