
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(1)求直线l被圆截得的弦长;
(2)从极点作圆C的弦,求各弦中点的极坐标方程.
【答案】
(1)解:依题,把直线l的参数方程化为普通方程为y= ![]() x,
x,
把圆C的极坐标方程化为直角坐标方程为x2+y2=4y,即x2+(y﹣2)2=4,…(3分)
则点C(0,2)到直线l的距离d= ![]() ,于是所求的弦长为
,于是所求的弦长为 ![]() ;
;
(2)解:记所作的弦为OA,设A(ρ0,θ0),弦OA的中点M(ρ,θ),
则 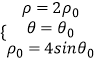 ,
,
消去ρ0,θ0,可得ρ=2sinθ即中点的极坐标方程.
【解析】(1)求出直线的普通方程,以及圆的普通方程,利用圆心到直线的距离以及半径半弦长的关系,求直线l被圆截得的弦长;(2)从极点作圆C的弦,设A(ρ0 , θ0),弦OA的中点M(ρ,θ),列出关系式,即可求各弦中点的极坐标方程.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】经市场调查,某旅游城市在过去的一个月内(以30天计),第t天(1≤t≤30,t∈N*)的旅游人数f(t)(单位:万人)近似地满足f(t)=4+ ![]() ,而人均日消费俄g(t)(单位:元)近似地满足g(t)=
,而人均日消费俄g(t)(单位:元)近似地满足g(t)= ![]() .
.
(1)试求所有游客在该城市旅游的日消费总额W(t)(单位:万元)与时间t(1≤t≤30,t∈N*)的函数表达式;
(2)求所有游客在该城市旅游的日消费总额的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
(1)求证:AD⊥BE
(2)求平面AEC和平面BDE所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①“已知函数y=f(x),x∈ D,若D关于原点对称,则函数y=f(x),x∈ D为奇函数”的逆命题;
②“对应边平行的两角相等”的否命题;
③“若a≠0,则方程ax+b=0有实根”的逆否命题;
④“若A∪ B=B,则B≠A”的逆否命题.
其中的真命题是( )
A. ①② B. ②③
C. ①③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列命题:①“若α=![]() ,则tan α=1”的逆否命题;②若f(x)=cos x,则f(x)为周期函数;③“若a=b,则|a|=|b|”的逆命题;④“若xy=0,则x,y中至少有一个为零”的否命题.其中真命题的序号是______.
,则tan α=1”的逆否命题;②若f(x)=cos x,则f(x)为周期函数;③“若a=b,则|a|=|b|”的逆命题;④“若xy=0,则x,y中至少有一个为零”的否命题.其中真命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=10n﹣n2(n∈N*),又bn=|an|(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com