解:(1)由题得a
n=q
n,∴b
n=a
n•log
4a
n=q
n•log
4q
n=n•5
n•log
45
∴S
n=(1×5+2×5
2+…+n×5
n)log
45
设T
n=1×5+2×5
2+…+n×5
n①
5T
n=1×5
2+2×5
3+…(n-1)5
n+n×5
n+1②
②-①:-4T
n=5+5
2+5
2+…+5
n-n×5
n+1=
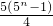
-n×5
n+1T
n=
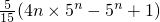
,
S
n=
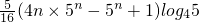
;
(2)b
n=a
nlog
4a
n=
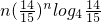
,
b
n+1-b
n=[(n+1)
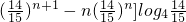
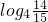
=
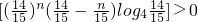
,因为
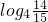
<0,
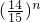
>0,
所以
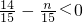
,解得n>14,
即取n≥15时,b
n<b
n+1.
所求的最小自然数是15.
分析:(1)根据数列{a
n}是首项、公比都为q的等比数列得到数列{a
n}的通项公式,把{a
n}的通项公式代入b
n=a
nlog
4a
n中得到数列{b
n}的通项公式,把q=5代入后列举出数列{b
n}的各项,提取log
45后剩下的式子设为T
n①,乘以5得到②,②-①再利用等比数列的前n项和的公式化简可得T
n的通项公式,即可得到数列{b
n}的前n项和S
n的通项公式;
(2)把q=
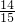
代入到b
n=a
nlog
4a
n中得到数列{b
n}的通项公式,然后根据b
n+1-b
n>0列出关于n的不等式,求出不等式的解集,即可找出满足题意的正整数n的值.
点评:此题考查学生掌握等比数列的性质,灵活运用等比数列的通项公式及前n项和的公式化简求值,会利用错位相减法求数列的和,是一道中档题.

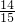 时,若bn<bn+1,求n最小值.
时,若bn<bn+1,求n最小值.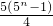 -n×5n+1
-n×5n+1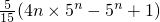 ,
,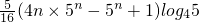 ;
;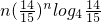 ,
,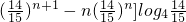
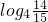
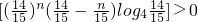 ,因为
,因为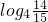 <0,
<0,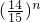 >0,
>0,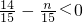 ,解得n>14,
,解得n>14,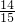 代入到bn=anlog4an中得到数列{bn}的通项公式,然后根据bn+1-bn>0列出关于n的不等式,求出不等式的解集,即可找出满足题意的正整数n的值.
代入到bn=anlog4an中得到数列{bn}的通项公式,然后根据bn+1-bn>0列出关于n的不等式,求出不等式的解集,即可找出满足题意的正整数n的值.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案