
(08年厦门外国语学校模拟)(12分)
已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 是它的两个焦点.
是它的两个焦点.
(Ⅰ)若椭圆上存在一点P,使得![]() 试求
试求![]() 的取值范围;
的取值范围;
(Ⅱ)若椭圆的离心率为![]() ,经过右焦点
,经过右焦点![]() 的直线
的直线![]() 与椭圆相交于A、B两点,且
与椭圆相交于A、B两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
解析:(Ⅰ)解法一:依题意得:![]() , ……………………………………………1分
, ……………………………………………1分
设![]() ,
,![]()
由![]() 得
得![]() ,即
,即![]() ,………………………2分
,………………………2分
又![]() , ∴
, ∴![]() . …………………………………………………4分
. …………………………………………………4分
∵![]() ∴
∴![]() ∴综上可得:
∴综上可得:![]() ……………6分
……………6分
解法二:设![]() ,
,![]()
![]() , …………………………………………………1分
, …………………………………………………1分
由![]() 得
得![]() ……………………………………2分
……………………………………2分
可得![]() , …………………………………………………4分
, …………………………………………………4分
下同解法一.
注:若设上顶点为B,根据![]() 得
得![]() ,即
,即![]()
因为![]() ,所以
,所以![]() 。此种解法给满分
。此种解法给满分
(Ⅱ)解法一:∵![]() ∴
∴![]() , ∴椭圆方程为
, ∴椭圆方程为![]() ,……7分
,……7分
依题意可设直线![]() 的方程为
的方程为![]()
由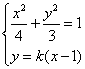 得
得![]()
设![]() ,则
,则![]() …………………8分
…………………8分
∵![]() ,∴
,∴![]() ………………………………9分
………………………………9分
∴![]()
![]() ,∴
,∴![]() ,
,![]() ……………10分
……………10分
∵![]() ,∴
,∴![]() ∴
∴![]() ………11分
………11分
所以直线![]() 的方程为
的方程为![]() ………………………………………………12分
………………………………………………12分
(Ⅱ)解法二:∵![]() ∴
∴![]() ,
,
∴椭圆方程为![]() , …………………………………………………………7分
, …………………………………………………………7分
设![]() ,∵
,∵![]() ,∴
,∴![]() ……8分
……8分
又![]() ,
,
可解得![]() ,即
,即![]() ………………………………11分
………………………………11分
所以![]()
所以直线![]() 的方程为
的方程为![]() ………………………………………………12分
………………………………………………12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:江西 题型:解答题
| 2an+1-an |
| 2an-an+1 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源:芜湖二模 题型:单选题
| A.16 | B.17 | C.18 | D.19 |
查看答案和解析>>
科目:高中数学 来源:安徽模拟 题型:填空题
| 3 |
| S1S3 |
| 15 |
| S3S5 |
| 5 |
| S5S1 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:惠州模拟 题型:单选题
|
|
|
|
| A.-2008 | B.2008 | C.2010 | D.-2010 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| an |
| an+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com