设函数
在
及
时取得极值．
（1）求a、b的值；（2）若对于任意的
，都有
成立，求c的取值范围．
阅读快车系列答案科目：高中数学 来源： 题型：解答题
某地政府为科技兴市，欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区（如图中阴影部分），形状为直角梯形QPRE（线段EQ和RP为两个底边），已知
其中AF是以A为顶点、AD为对称轴的抛物线段．试求该高科技工业园区的最大面积．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
，
.
（1）若
，则
，
满足什么条件时，曲线
与
在
处总有相同的切线？
（2）当
时，求函数
的单调减区间；
（3）当
时，若
对任意的
恒成立，求的取值的集合.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
，
，
，其中
，且
.
⑴当
时，求函数
的最大值；
⑵求函数
的单调区间；
⑶设函数
若对任意给定的非零实数
，存在非零实数
（
），使得
成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
（
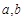为常数），其图象是曲线
．
（1）当
时，求函数
的单调减区间；
（2）设函数的导函数为
，若存在唯一的实数
，使得
与
同时成立，求实数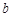
的取值范围；
（3）已知点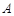
为曲线上的动点，在点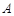处作曲线的切线
与曲线交于另一点
，在点处作曲线的切线
，设切线
的斜率分别为
．问：是否存在常数
，使得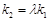
？若存在，求出的值；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
；（2）
，可得
，又函数
在
，即
，从而解得
，
，则
，
上的最大值为
都有
，从而可求出
的取值范围为
．
在x=l和x=3处的切线互相平行，求a的值及函数
的单调区间；
，若对任意
，均存在
，使得
，求实数a的取值范围．
.
，函数
在区间
上是单调递增函数，求实数
的取值范围；
，若对任意
恒成立，求
,
(
).
的单调区间；
时,对于任意
,总有
成立．
.
在区间
单调递增，求
的最小值；
，对
，使
成立，求
的范围.