
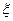 的分布列及数学期望E
的分布列及数学期望E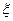 。
。 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资. ,求
,求 的分布列及数学期望E
的分布列及数学期望E .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券. 张奖券中奖,求
张奖券中奖,求 的分布列,并求
的分布列,并求 的数学
的数学查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


 的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?
的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
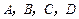 四个交通岗,其中在
四个交通岗,其中在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 ,在
,在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 .假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数.
.假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数. ,就会迟到,求张华不迟到的概率;(2)求EX.
,就会迟到,求张华不迟到的概率;(2)求EX.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的概率分布列及数学期望。
的概率分布列及数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.np(1-p) | B.np | C.n | D.p(1-p) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com