
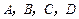 四个交通岗,其中在
四个交通岗,其中在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 ,在
,在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 .假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数.
.假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数. ,就会迟到,求张华不迟到的概率;(2)求EX.
,就会迟到,求张华不迟到的概率;(2)求EX.科目:高中数学 来源:不详 题型:解答题
 ,若中奖,则家具城返还顾客现金1000元,某顾客购买一张价格为3400元的餐桌,
,若中奖,则家具城返还顾客现金1000元,某顾客购买一张价格为3400元的餐桌, 元;
元; 的所有可能取值;
的所有可能取值; 的分布列;
的分布列; 的期望E(
的期望E( );
);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高180元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等概率的.请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高180元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等概率的.请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
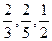 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 2,机器发生故障时全天停止工作
2,机器发生故障时全天停止工作 若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?
若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 自然状况 | 方案甲 | 方案乙 | 方案丙 | |||
| 概率 | 获利 (万元) | 概率 | 获利 (万元) | 概率 | 获利 (万元) | |
| 巨大成功 | 0.4 | 6 | 0.3 | 7 | 0.4 | 6.5 |
| 中等成功 | 0.3 | 2 | 0.4 | 2.5 | 0.2 | 4.5 |
| 不成功 | 0.3 | -4 | 0.3 | -5 | 0.4 | -4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com