【题目】已知二次函数满足（），且．

（1）求的解析式；

（2）若函数在区间上是单调函数，求实数的取值范围；

（3）若关于的方程有区间上有一个零点，求实数的取值范围．

参考答案：

【答案】（1）；（2）；（3）．

【解析】

试题分析：（1）设（）代入得对于恒成立，列出方程，求得的值，即可求解函数的解析式；（2）由，根据函数在上是单调函数，列出不等式组，即可求解实数的取值范围；（3）由方程得，令，即要求函数在上有唯一的零点，分类讨论即可求解实数的取值范围．

试题解析：（1）设（）代入得

对于恒成立，故，

又由得，解得，，，所以；

（2）因为，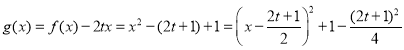

又函数在上是单调函数，故或，

解得或，故实数的取值范围是；

（3）由方程得，

令，，即要求函数在上有唯一的零点，

①，则，代入原方程得或3，不合题意；

②若，则，代入原方程得或2，满足题意，故成立；

③若，则，代入原方程得，满足题意，故成立；

④若且且时，由得，

综上，实数的取值范围是．

关闭