练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．设集合M={x|x2＜x}，N={x||x|＜1}，则（　　）
    A．M∩N=∅B．M∪N=MC．M∩N=MD．M∪N=R

    分析 解x2＜x可得集合M={x|0＜x＜2}，解|x|＜1可得集合N，由交集的定义，分析可得答案．

    解答 解：x2＜x?0＜x＜1，则集合M={x|0＜x＜1}，
    |x|＜1?-1＜x＜1，则集合N={x|-1＜x＜1}，
    则M∩N={x|0＜x＜1}=M，
    故选C．

    点评 本题考查集合交集的计算，关键是求出集合集合M、N．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．在△ABC中，已知$cosA=\frac{3}{5}，cosB=\frac{5}{13}$，AC=3，则AB=$\frac{14}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设等差数列{an}的前n项和为Sn，a22=37，S22=352．
    （1）求数列{an}的通项公式；
    （2）若bn=$\frac{1}{{a}_{n+3}•{a}_{n+4}}$，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．△ABC的内角A、B、C的对边分别为a，b，c，且a≠b，则$\frac{sinC（bcosA-acosB）}{asinA-bsinB}$=（　　）
    A．-1B．-2C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两焦点分别为F1，F2，点D是椭圆C上一动点当△DF1F2的面积取得最大值1时，△DF1F2为直角三角形．
    （1）椭圆C的方程．
    （2）已知点P是椭圆C上的一点，则过点P（x0，y0）的切线的方程为$\frac{x{x}_{0}}{{a}^{2}}$+$\frac{y{y}_{0}}{{b}^{2}}$=1．过直线l：x=2上的任意点M引椭圆C的两条切线，切点分别为A，B，求证：直线AB恒过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．角α的顶点与直角坐标系的原点重合，始边与x轴的非负半轴重合，“角α的终边在射线x+3y=0（x≥0）上”是“sin2α=-$\frac{3}{5}$”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

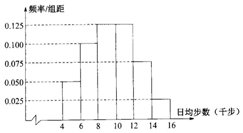    10．某单位委托一家网络调查公司对单位1000名职员进行了QQ运动数据调查，绘制了日均行走步数（千步）的频率分布直方图，如图所示（每个分组包括左端点，不包括右端点，如第一组表示运动量在[4，6）之间（单位：千步））．
    （1）求单位职员日均行走步数在[6，8）的人数．
    （2）根据频率分布直方图算出样本数据的中位数；
    （3）若将频率视为概率，从本单位随机抽取3位职员（看作有放回的抽样），求日均行走步数在[10，14）的职员数X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．狄利克雷是德国著名数学家，函数D（x）=$\left\{\begin{array}{l}{1，x为有理数}\\{0，x为无理数}\end{array}\right.$被称为狄利克雷函数，下面给出关于狄利克雷函数D（x）的五个结论：
    ①若x是无理数，则D（D（x））=0；
    ②函数D（x）的值域是[0，1]；
    ③函数D（x）偶函数；
    ④若T≠0且T为有理数，则D（x+T）=D（x）对任意的x∈R恒成立；
    ⑤存在不同的三个点A（x1，D（x1）），B（x2，D（x2）），C（x3，D（x3）），使得△ABC为等边角形．
    其中正确结论的序号是②③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若集合A={0，1，2，3，4，6}，集合B={y|y=2x，x∈A}，则A∩B的元素个数为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    同步练习册答案