
【题目】已知函数f(x)=2cos22x﹣2,给出下列命题: ①β∈R,f(x+β)为奇函数;
②α∈(0, ![]() ),f(x)=f(x+2α)对x∈R恒成立;
),f(x)=f(x+2α)对x∈R恒成立;
③x1 , x2∈R,若|f(x1)﹣f(x2)|=2,则|x1﹣x2|的最小值为 ![]() ;
;
④x1 , x2∈R,若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z).其中的真命题有( )
A.①②
B.③④
C.②③
D.①④
【答案】C
【解析】解:由题意,f(x)=2cos22x﹣2=cos4x﹣1; 对于①,∵f(x)=cos4x﹣1的图象如图所示;
函数f(x+β)的图象是f(x)的图象向左或向右平移|β|个单位,
它不会是奇函数的,故①错误;
对于②,f(x)=f(x+2α),∴cos4x﹣1=cos(4x+8α)﹣1,
∴8α=2kπ,∴α= ![]() ,k∈Z;
,k∈Z;
又α∈(0, ![]() ),∴取α=
),∴取α= ![]() 或
或 ![]() 时,
时,
∴f(x)=f(x+2α)对x∈R恒成立,②正确;
对于③,|f(x1)﹣f(x2)|=|cos4x1﹣cos4x2|=2时,
|x1﹣x2|的最小值为 ![]() =
= ![]() =
= ![]() ,∴③正确;
,∴③正确;
对于④,当f(x1)=f(x2)=0时,
x1﹣x2=kT=k ![]() =
= ![]() (k∈Z),∴④错误;
(k∈Z),∴④错误;
综上,真命题是②③.
故选:C.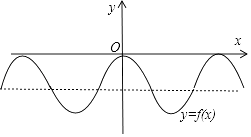
化简函数f(x),画出f(x)的图象,根据图象平移判断函数f(x+β)不是奇函数,判断①错误;
根据f(x)=f(x+2α)求出方程在α∈(0, ![]() )的解,判断②正确;
)的解,判断②正确;
由|f(x1)﹣f(x2)|=2时,|x1﹣x2|的最小值为 ![]() =
= ![]() ,判断③正确;
,判断③正确;
当f(x1)=f(x2)=0时,x1﹣x2=kT= ![]() ,判断④错误.
,判断④错误.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=2,a4=14,数列{bn}满足b1=1,b4=6,且{an﹣bn}是等比数列. (Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)若n∈N* , 都有bn≤bk成立,求正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xln(x﹣1)﹣a(x﹣2). (Ⅰ)若a=2017,求曲线f(x)在x=2处的切线方程;
(Ⅱ)若当x≥2时,f(x)≥0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() 在(0,2)上存在两个极值点,则a的取值范围是( )
在(0,2)上存在两个极值点,则a的取值范围是( )
A.(﹣∞,﹣ ![]() )
)
B.(﹣∞,﹣ ![]() )
)
C.(﹣∞,﹣ ![]() )∪(﹣
)∪(﹣ ![]() ,﹣
,﹣ ![]() )
)
D.(﹣e,﹣ ![]() )∪(1,+∞)
)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=eax(a≠0).
(1)当 ![]() 时,令
时,令 ![]() (x>0),求函数g(x)在[m,m+1](m>0)上的最小值;
(x>0),求函数g(x)在[m,m+1](m>0)上的最小值;
(2)若对于一切x∈R,f(x)﹣x﹣1≥0恒成立,求a的取值集合;
(3)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE. 
(1)求BM的长;
(2)求二面角A﹣DM﹣B的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+2= ![]() ,n∈N*,且a1=1,a2=2.
,n∈N*,且a1=1,a2=2.
(1)求数列{an}的通项公式;
(2)令bn=(﹣1)nanan+1 , n∈N*,求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com