
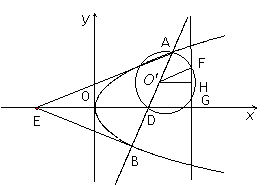
(09年莱西一中模拟理)(14分)已知点H(-3,0),点P在![]() 轴上,点Q在
轴上,点Q在![]() 轴的正半轴上,点M在直线PQ上,且满足
轴的正半轴上,点M在直线PQ上,且满足![]() ,
, ![]()
![]() .
.
(Ⅰ)当点P在![]() 轴上移动时,求点M的轨迹C;
轴上移动时,求点M的轨迹C;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证:
交轨迹C于A、B两点,E是D点关于坐标原点O的对称点,求证:![]() ;
;
(Ⅲ)在(Ⅱ)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以AD为直径的圆截得的弦长恒为定值?若存在求出
被以AD为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

解析:(Ⅰ)设![]() ,
,
![]()
![]()
![]() 且
且![]() , …………………2分
, …………………2分
![]() …………………3分
…………………3分
![]() . ………………………………………………4分
. ………………………………………………4分
∴动点M的轨迹C是以O(0,0)为顶点,以(1,0)为焦点的抛物线(除去原点).
…………………………………………5分
(Ⅱ)解法一:(1)当直线![]() 垂直于
垂直于![]() 轴时,根据抛物线的对称性,有
轴时,根据抛物线的对称性,有![]() ;
;
……………6分
(2)当直线![]() 与
与![]() 轴不垂直时,依题意,可设直线
轴不垂直时,依题意,可设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组

消去![]() 并整理,得
并整理,得
![]() ,
,
![]() . ……………7分
. ……………7分
设直线AE和BE的斜率分别为![]() ,则:
,则:
![]() =
=![]()
![]()
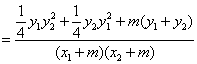
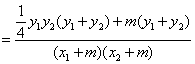
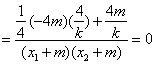 . …………………9分
. …………………9分
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() .
.
综合(1)、(2)可知![]() . …………………10分
. …………………10分
解法二:依题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组:
,则A,B两点的坐标满足方程组:
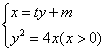
消去![]() 并整理,得
并整理,得
![]() ,
,
![]() . ……………7分
. ……………7分
设直线AE和BE的斜率分别为![]() ,则:
,则:
![]() =
=![]()
![]()
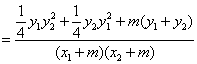
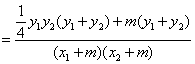
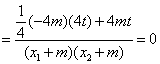 . …………………9分
. …………………9分
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() . ……………………………………………………10分
. ……………………………………………………10分
(Ⅲ)假设存在满足条件的直线![]() ,其方程为
,其方程为![]() ,AD的中点为
,AD的中点为![]() ,
,![]() 与AD为直径的圆相交于点F、G,FG的中点为H,则
与AD为直径的圆相交于点F、G,FG的中点为H,则![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() . …………………………12分
. …………………………12分
![]() ,
,
令![]() ,得
,得![]()
此时,![]() .
.
∴当![]() ,即
,即![]() 时,
时,![]() (定值).
(定值).
∴当![]() 时,满足条件的直线
时,满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ;当
;当![]() 时,满足条件的直线
时,满足条件的直线![]() 不存在.
不存在.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
(09年莱西一中模拟理)(12分)
设![]() 是函数
是函数![]() 的一个极值点.
的一个极值点.
(Ⅰ)求![]() 与
与![]() 的关系式(用
的关系式(用![]() 表示
表示![]() ),并求
),并求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,使得
,使得![]() 成立?若存在,求
成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年莱西一中模拟文)(12分)某工厂统计资料显示,产品次品率![]() 与日产量
与日产量![]() (单位件,
(单位件,![]() ,
,![]() )的关系如下:
)的关系如下:
| 1 | 2 | 3 | 4 | … | 96 |
|
|
|
|
| … |
|
又知每生产一件正品盈利![]() (
(![]() 为正常数)元,每生产一件次品就损失
为正常数)元,每生产一件次品就损失![]() 元.
元.
(Ⅰ)将该厂日盈利额![]() (元)表示为日产量
(元)表示为日产量![]() 的函数;
的函数;
(Ⅱ)为了获得最大赢利,该厂的日产量应定为多少件?
(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年莱西一中模拟理)(12分)
已知将一枚质地不均匀的硬币抛掷三次,三次正面均朝上的概率为![]()
(1)求抛掷这样的硬币三次,恰有两次正面朝上的概率;
(2)抛掷这样的硬币三次后,抛掷一枚质地均匀的硬币一次,记四次抛掷后正面朝上的总次数为ξ,求随机变量ξ的分布列及期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年莱西一中模拟)(12分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为![]() m,圆环的圆心距离地面的高度为
m,圆环的圆心距离地面的高度为![]() ,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
(1)试确定在时刻t时蚂蚁距离地面的高度![]() ;
;
(2)画出函数![]() 在
在![]() 时的图象;
时的图象;
(3)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过![]() m?
m?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com