练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知双曲线的一条渐近线方程为，

    则该双曲线的离心率为      ．


     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    （Ⅰ）已知函数f(x)＝ex－1－tx，∃x0∈R，使f(x0)≤0，求实数t的取值范围；

    （Ⅱ）证明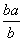：＜ln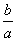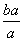＜，其中0＜a＜b；

    （Ⅲ）设[x]表示不超过x的最大整数，证明：[ln(1＋n)]≤[1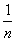＋＋…＋]≤1＋[lnn]（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


      如图，在正三棱柱中，所有棱长都相等，点分别是与的中点．

    （1）求证：平面平面；

    （2）若点在棱上，且，求证：平面平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数，则满足不等式的的取值范围是 。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


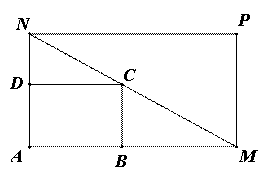
    如图，将一矩形花坛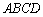扩建成一个更大的矩形花坛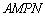,要求M在AB的延长线上，N在AD的延长线上，且对角线MN过点C。已知AB=2米，AD=1米。

      ⑴设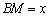（单位：米），要使花坛AMPN的面积大于9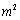，求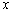的取值范围。

      ⑵若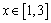（单位：米），则当AM,AN的长分别是多少时，花坛AMPN的面积最大？并求出最大面积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数，则不等式的解集为     ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


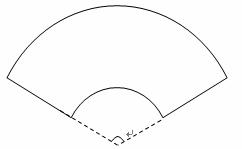
    某单位拟建一个扇环面形状的花坛(如图所示)，该扇环面是由以点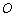为圆心的两个同心圆弧和延长后通过点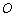的两条直线段围成．按设计要求扇环面的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为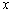米，圆心角为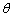（弧度）．

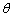    （1）求关于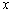的函数关系式；

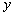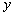    （2）已知在花坛的边缘(实线部分)进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为，求关于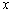的函数关系式，并求出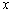为何值时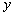，取得最大值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若圆与圆相交，则实数的取值范围是

           　　　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    根据如图所示的伪代码，可知输出S的值为         .

    查看答案和解析>>

    同步练习册答案