用绳子围成一块矩形场地,若绳长为40米,则围成矩形的最大面积是 平方米.
【答案】
分析:设矩形的一个边长为x,建立函数关系,然后利用函数的性质求最大值.
解答:解:要使围成的矩形的面积最大,则绳子没有剩余.
设矩形的一个边长为x,则两外一个边长为
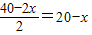
,由20-x>0,
得0<x<20.
所以矩形的面积为S=x(20-x)=-x
2+20x=-(x-10)
2+100,
所以当x=10米时,矩形面积的最大值为100平方米.
故答案为:100.
点评:本题主要考查函数的应用,利用二次函数的性质是解决本题的关键.
