数列{an}的前n项和为Sn,数列{bn}的前n项的和为Tn,{bn}为等差数列且各项均为正数,a1=1,an+1=2Sn+1(n∈N+),b1+b2+b3=
15.
(1)求证:数列{an}是等比数列;
(2)若a1+b1,a2+b2,a3+b3成等比数列,求Tn.
解:(1)当n≥2时,a
n+1-a
n=(2S
n+1)-(2S
n-1+1)=2a
n.
∴a
n+1=3a
n,即
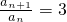
…4分
又 a
2=2S
1+1=3=3a
1 …2分
∴{a
n}是公比为3的等比数列 …8分
(2)由(1)得:a
n=3
n-1 …9分
设{b
n}的公差为d(d>0),∵T
3=15,∴b
2=5 …11分
依题意a
1+b
1,a
2+b
2,a
3+b
3成等比数列,有(a
2+b
2)
2=(a
1+b
1)(a
3+b
3),
∴64=(5-d+1)(5+d+9)
d
2+8d-20=0,得d=2,或d=-10(舍去) …14分
故T
n=3n+
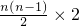
=n
2+2n …16分.
分析:(1)通过a
n+1-a
n=(2S
n+1)-(2S
n-1+1)=2a
n.利用等比数列的定义判断{a
n}是公比为3的等比数列.
(2)由(1)得数列{a
n}通项公式,设{b
n}的公差为d(d>0),利用a
1+b
1,a
2+b
2,a
3+b
3成等比数列,求出公差,然后求解T
n.
点评:本题考查等比数列的性质,等差数列的前n项和,等比关系的确定的应用,考查计算能力.

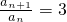 …4分
…4分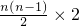 =n2+2n …16分.
=n2+2n …16分.
