
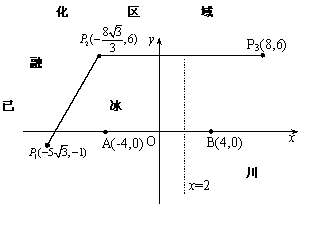
为了考察冰川的融化状况,一支科考队在某冰川上相距8km的A,B两点各建一个考察基地.视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(图).在直线![]() 的右侧,考察范围为到点B的距离不超过
的右侧,考察范围为到点B的距离不超过![]() km的区域;在直线
km的区域;在直线![]() 的左侧,考察范围为到A,B两点的距离之和不超过
的左侧,考察范围为到A,B两点的距离之和不超过![]() km的区域.
km的区域.
(1)求考察区域边界曲线的方程;
(2)如图所示,设线段![]() ,
,![]() 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间.
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间.
 |
解(1)设边界曲线上点P的坐标为![]() .当
.当![]() 时,由题意知
时,由题意知![]() .
.
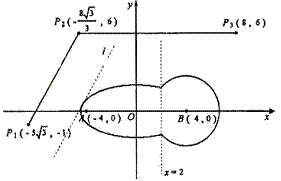 当
当![]() 时,由
时,由![]() 知,点P在以
知,点P在以![]() 为焦点,
为焦点,
长轴长为![]() 的椭圆上.
的椭圆上.
此时短半轴长![]() .
.
因而其方程为![]() .
.
故考察区域边界曲线(如图)的方程为
![]() 和
和![]() .
.
(2)设过点![]() 的直线为
的直线为![]() ,过点
,过点![]() 的直线为
的直线为![]() ,则直线
,则直线![]() ,
,![]() 的方程分别为
的方程分别为
![]()
设直线![]() 平行于直线
平行于直线![]() ,其方程为
,其方程为![]() 代入椭圆方程
代入椭圆方程![]() ,
,
消去![]() ,得
,得![]() .
.
由![]() ,解得
,解得![]() ,或
,或![]() .
.
从图中可以看出,当![]() 时,直线
时,直线![]() 与
与![]() 的公共点到
的公共点到![]() 的距离最近,此时直线
的距离最近,此时直线![]()
的方程为![]()
![]() 与
与![]() 之间的距离为
之间的距离为![]() .
.
又直线![]() 到
到![]() 和
和![]() 的最短距离
的最短距离![]() 而
而![]() ,所以考察区域边界到冰川边界线的最短距离为3.设冰川边界线移动到考察区域所需的时间为
,所以考察区域边界到冰川边界线的最短距离为3.设冰川边界线移动到考察区域所需的时间为![]() 年,
年,
则由题设及等比数列求和公式,得![]() ,所以
,所以![]() .
.
故冰川边界线移动到考察区域所需的时间为4年.


科目:高中数学 来源: 题型:
6
| ||
| 5 |
| 5 |
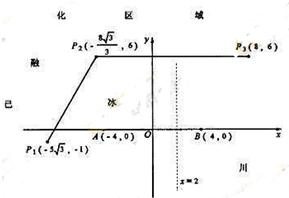
查看答案和解析>>
科目:高中数学 来源: 题型:
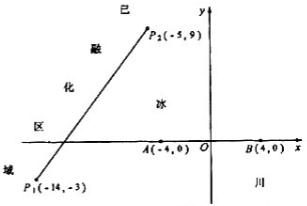 为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域.
为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域.查看答案和解析>>
科目:高中数学 来源:湖南省高考真题 题型:解答题
 km的区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过4
km的区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过4 km的区域,
km的区域, 
查看答案和解析>>
科目:高中数学 来源:湖南省高考真题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:圆锥曲线(2)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com