
 图象的对称中心是(1,1);
图象的对称中心是(1,1);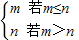 ,则函数f(x)=
,则函数f(x)= 的值域为(-∞,0];
的值域为(-∞,0];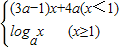 对任意的x1≠x2都有
对任意的x1≠x2都有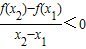 ,则实数a的取值范围是(-
,则实数a的取值范围是(- ,1],
,1],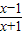 =
=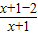 =1-
=1-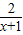 ,∵y=
,∵y=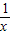 的对称中心为(0,0),∴y=1-
的对称中心为(0,0),∴y=1-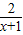 的对称中心为(-1,1),故①不正确.
的对称中心为(-1,1),故①不正确.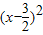 -
- ,当x>2时,
,当x>2时,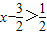 ,
,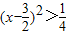 ,∴x2-3x+2=
,∴x2-3x+2=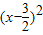 -
- >0,∴x>2 是x2-3x+2>0的充分条件,由x2-3x+2>0得x<1或x>2,故由x2-3x+2>0不一定推得x>2,∴是不必要的条件,故②正确.
>0,∴x>2 是x2-3x+2>0的充分条件,由x2-3x+2>0得x<1或x>2,故由x2-3x+2>0不一定推得x>2,∴是不必要的条件,故②正确.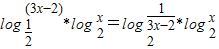 定义域为{x|x>
定义域为{x|x> },由m*n=
},由m*n=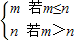 知f(x)=
知f(x)=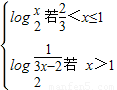 ,解得f(x)∈(-∞,0],故③正确.
,解得f(x)∈(-∞,0],故③正确.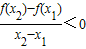 知f(x)为定义域上的减函数,要使f(x)=
知f(x)为定义域上的减函数,要使f(x)=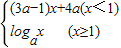 在定义域内为减函数,则
在定义域内为减函数,则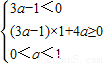 ,解得
,解得 ,故④不正确.
,故④不正确.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| ω |
| 2 |
| 3 |
| 5 |
| 2 |
| π |
| 8 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| a |
| A、①③ | B、②③ | C、①② | D、③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com