
【题目】在四菱锥P﹣ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
(I)求证:PA⊥AB;
(II)求直线AD与平面PCD所成角的大小.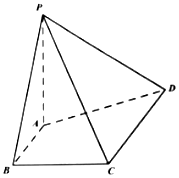
【答案】证明:(I)取CD的中点E,连接AE,PE,则AE⊥CD,PE⊥CD, ∵AE∩PE=E,∴CD⊥平面PAE.
∵PA平面PAE,∴CD⊥PA,
∵PA⊥AD,AD∩CD=D,
∴PA⊥平面ABCD,
∵AB平面ABCD,
∴PA⊥AB;
(II)解:由题意,AD=PE= ![]() .
.
设A到平面PCD的距离为h,则由等体积可得 ![]() =
= ![]() ,
,
∴h= ![]()
∴直线AD与平面PCD所成角的正弦值为 ![]() =
= ![]() ,大小为30°.
,大小为30°.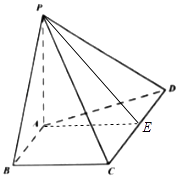
【解析】(I)取CD的中点E,连接AE,PE,则AE⊥CD,PE⊥CD,证明PA⊥平面ABCD,即可证明:PA⊥AB;(II)求出A到平面PCD的距离,即可求直线AD与平面PCD所成角的大小.
【考点精析】关于本题考查的直线与平面垂直的性质和空间角的异面直线所成的角,需要了解垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则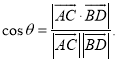 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() ),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
A.[ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数,﹣π<α<0),曲线C2的参数方程为
(α为参数,﹣π<α<0),曲线C2的参数方程为  (t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1的极坐标方程和曲线C2的普通方程;
(2)射线θ=﹣ ![]() 与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣
(a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣ ![]() ,则P到直线QM的距离为
,则P到直线QM的距离为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-5:不等式选讲】
已知f(x)=|x﹣1|+|x+2|.
(I)若不等式f(x)>a2对任意实数x恒成立,求实数a的取值的集合T;
(Ⅱ)设m、n∈T,证明: ![]() |m+n|<|mn+3|.
|m+n|<|mn+3|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品计划提价,现有四种方案,方案(Ⅰ)先提价m%,再提价n%;方案(Ⅱ)先提价n%,再提价m%;方案(Ⅲ)分两次提价,每次提价( ![]() )%;方案(Ⅳ)一次性提价(m+n)%,已知m>n>0,那么四种提价方案中,提价最多的是( )
)%;方案(Ⅳ)一次性提价(m+n)%,已知m>n>0,那么四种提价方案中,提价最多的是( )
A.Ⅰ
B.Ⅱ
C.Ⅲ
D.Ⅳ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AC⊥AB,AB=2AA1 , M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
(Ⅰ)若DE∥平面A1MC1 , 求 ![]() ;
;
(Ⅱ)求直线BG和平面A1MC1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x ln x﹣ax2+(2a﹣1)x,a∈R.
(Ⅰ)令g(x)=f′(x ),求 g(x)的单调区间;
(Ⅱ)当a≤0时,直线 y=t(﹣1<t<0)与f(x)的图象有两个交点A(x1 , t),B(x2 , t),且x1<x2 , 求证:x1+x2>2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com