已知数列{an}中,a1=4,a2=6,且an+1=4an-3an-1(n≥2),设bn=an+1-an,
(1)求证数列{bn}成等比数列;
(2)求m的值及{cn}的前n项和.
(1)证明:∵a
n+1=4a
n-3a
n-1(n≥2),∴a
n+1-a
n=3(a
n-a
n-1),
∵b
n=a
n+1-a
n,
∴b
n=3b
n-1(n≥2),
∵b
1=a
2-a
1=2
∴数列{b
n}是以2为首项,3为公比的等比数列,通项公式为b
n=2×3
n-1;
(2)解:由(1)知,a
n=a
1+(a
2-a
1)+…+(a
n-a
n-1)=4+2+…+2×3
n-1=3
n-1+3
∵
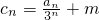
∴
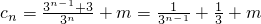
∵数列{c
n}成等比数列
∴
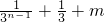
=

(n≥2)
∴3q=1
∴q=

∴
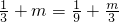
∴
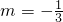
∴{c
n}的前n项和为
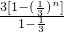
=
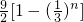
分析:(1)利用a
n+1=4a
n-3a
n-1(n≥2),可得a
n+1-a
n=3(a
n-a
n-1),从而可得数列{b
n}的通项公式;
(2)由(1)知,a
n=a
1+(a
2-a
1)+…+(a
n-a
n-1)=4+2+…+2×3
n-1=3
n-1+3,再利用数列{c
n}成等比数列,可求m的值,从而可求c
n}的前n项和.
点评:本题考查数列的通项,考查数列的求和,正确运用数列递推式是关键.

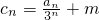
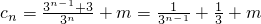
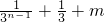 =
= (n≥2)
(n≥2)
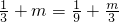
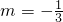
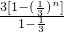 =
=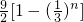


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案