
解析:本题可以使用直线的普通方程来解,也可以使用参数方程来解,但是使用普通方程解,运算较为麻烦.如果设出直线的倾斜角,写出直线的参数方程来解,就可以把问题转化为三角函数的最小值问题,便于计算.
解:设直线的倾斜角为α,则它的方程为![]() (t为参数),由A、B是坐标轴上的点知yA=0,xB=0,?
(t为参数),由A、B是坐标轴上的点知yA=0,xB=0,?
∴0=2+tsinα,即|PA|=|t|=![]() ;0=3+tcosα,即|PB|=|t|=-
;0=3+tcosα,即|PB|=|t|=-![]() 故|PA|·|PB|=
故|PA|·|PB|=![]() ∵90°<α<180°,∴当2α=270°,即α=135°时,|PA|·|PB|有最小值.∴直线方程为
∵90°<α<180°,∴当2α=270°,即α=135°时,|PA|·|PB|有最小值.∴直线方程为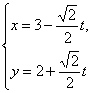 (t为参数),化为普通方程即x+y-5=0.
(t为参数),化为普通方程即x+y-5=0.
点评:直线的参数方程和普通方程可以进行互化,特别是要求直线上某一定点到直线与曲线交点距离时通常要使用参数的几何意义,宜用参数方程的标准形式,而对于某些比较简单的直线问题比如求直线和坐标轴或者与某条直线交点时宜用直线的普通方程.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com