
已知函数
(1)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;
(2)判断函数f(x)的单调性;
(3)求证: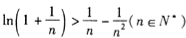
(1) 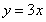 ;(2) 参考解析;(3)参考解析
;(2) 参考解析;(3)参考解析
【解析】
试题分析:(1)已知函数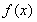 是一个 含对数与分式,以及复合函数,需要正确地对函数
是一个 含对数与分式,以及复合函数,需要正确地对函数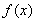 求导,因为函数在x=0处的切线方程,所以将x=0代入导函数,即可求出切线的斜率.再根据横坐标为0,计算出纵坐标,根据点斜式即可写出切线方程.
求导,因为函数在x=0处的切线方程,所以将x=0代入导函数,即可求出切线的斜率.再根据横坐标为0,计算出纵坐标,根据点斜式即可写出切线方程.
(2)需要判断函数的单调性,要对函数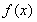 求导,判断导函数的值的正负,所以要根据参数
求导,判断导函数的值的正负,所以要根据参数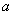 的情况分类讨论后作出判定.
的情况分类讨论后作出判定.
(3)解法(一)令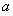 为特殊值,通过函数的单调性得到一个不等式成立,再将x转化为数列中的n的相关的值,再利用一个不等式,从而得到结论.解法(二)根据结论构造函数,通过函数的最值证明恒成立,再将x转化为n的表达式即可.
为特殊值,通过函数的单调性得到一个不等式成立,再将x转化为数列中的n的相关的值,再利用一个不等式,从而得到结论.解法(二)根据结论构造函数,通过函数的最值证明恒成立,再将x转化为n的表达式即可.
试题解析:(1)当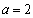 时,
时,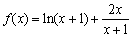 ,
,
∴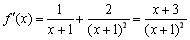 ,
,
∴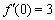 ,所以所求的切线的斜率为3.又∵
,所以所求的切线的斜率为3.又∵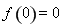 ,所以切点为
,所以切点为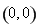 . 故所求的切线方程为:
. 故所求的切线方程为: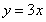 .
.
(2)∵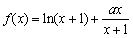
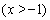 ,
,
∴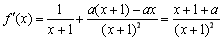 . ①当
. ①当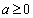 时,∵
时,∵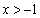 ,∴
,∴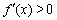 ; 7分
; 7分
②当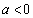 时,
时,
由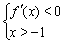 ,得
,得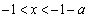 ;由
;由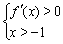 ,得
,得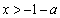 ; 综上,当
; 综上,当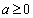 时,函数
时,函数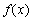 在
在 单调递增;
单调递增;
当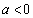 时,函数
时,函数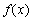 在
在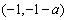 单调递减,在
单调递减,在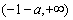 上单调递增.
上单调递增.
(3)方法一:由(2)可知,当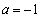 时,
时,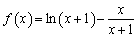 在
在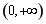 上单调递增. ∴ 当
上单调递增. ∴ 当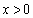 时,
时,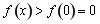 ,即
,即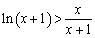 . 令
. 令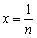 (
(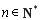 ),则
),则 . 另一方面,∵
. 另一方面,∵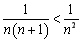 ,即
,即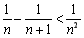 ,
,
∴ 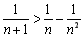 . ∴
. ∴ 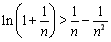 (
(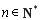 ). 方法二:构造函数
). 方法二:构造函数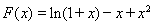 ,
,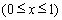 ∴
∴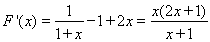 , ∴当
, ∴当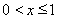 时,
时,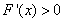 ;
;
∴函数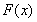 在
在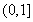 单调递增. ∴函数
单调递增. ∴函数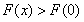 ,即
,即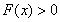
∴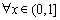 ,
,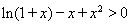 ,即
,即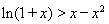
令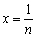 (
(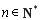 ),则有
),则有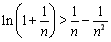 .
.
考点:1.函数的导数的几何意义.2.函数的单调性.3.函数与数列的知识交汇.4.构造新函数的思想.5.运算能力.


科目:高中数学 来源:安徽省桐城十中2012届高三上学期第一次月考数学理科试题 题型:044
已知函数![]() .
.
(1)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求函数y=f(x)的单调区间;
(2)若对于![]() 都有f(x)>2(a-1)成立,试求的取值范围;
都有f(x)>2(a-1)成立,试求的取值范围;
(3)记g(x)=f(x)+x-b(b∈R).当a=1时,函数g(x)在区间[e-1,e]上有两个零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:解答题
已知函数f(x)=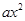 -(a+2)x+lnx.
-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e)上的最小值为-2,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期第一次调研考试数学试卷(实验班) 题型:解答题
(本小题14分)已知函数f(x)=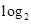 (x+
(x+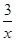 -a)的定义域为A,值域为B.
-a)的定义域为A,值域为B.
(1)当a=4时,求集合A;
(2)当B=R时,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com