
定义“正对数”: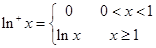 ,现有四个命题:
,现有四个命题:
①若 ,则
,则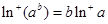
②若 ,则
,则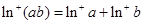
③若 ,则
,则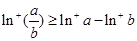
④若 ,则
,则
其中的真命题有:__________.(写出所有真命题的编号)
科目:高中数学 来源: 题型:填空题
下列四个命题中,真命题的序号有 .(写出所有真命题的序号)
①若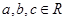 ,则“
,则“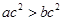 ”是“
”是“ ”成立的充分不必要条件;
”成立的充分不必要条件;
②命题“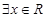 使得
使得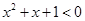 ”的否定是“
”的否定是“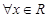 均有
均有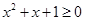 ”;
”;
③命题“若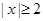 ,则
,则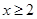 或
或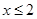 ”的否命题是“若
”的否命题是“若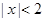 ,则
,则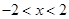 ”;
”;
④函数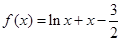 在区间
在区间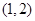 上有且仅有一个零点.
上有且仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知命题p:?x∈R,使tanx=1,命题q:x2-3x+2<0的解集是{x|1<x<2}.下列结论:①命题“p∧q”是真命题; ②命题“p∧( q)”是假命题;③命题“(
q)”是假命题;③命题“( p)∨q”是真命题;④命题“(
p)∨q”是真命题;④命题“( p)∨(
p)∨( q)”是假命题.其中正确的是________.(填所有正确命题的序号)
q)”是假命题.其中正确的是________.(填所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知a,b,c∈R,命题“若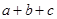 =3,则
=3,则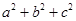 ≥3”,的否命题是 ( )
≥3”,的否命题是 ( )
A.若a+b+c≠3,则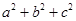 <3 <3 | B.若a+b+c=3,则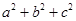 <3 <3 |
C.若a+b+c≠3,则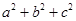 ≥3 ≥3 | D.若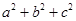 ≥3,则a+b+c=3 ≥3,则a+b+c=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设函数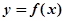 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足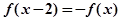 对一切
对一切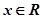 恒成立,当
恒成立,当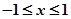 时,
时,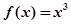 。则下列四个命题中正确的命题是
。则下列四个命题中正确的命题是
①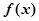 是以4为周期的周期函数;②
是以4为周期的周期函数;②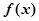 在
在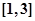 上的解析式为
上的解析式为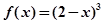 ;③
;③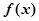 的图象的对称轴中有
的图象的对称轴中有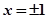 ;④
;④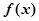 在
在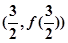 处的切线方程为
处的切线方程为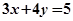 。
。
| A.①②③ | B.②③④ | C.①③④ | D.①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com