练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知an=-n2+9n+10(n∈N*)是数列{an}的通项公式.求:

    (1)数列{an}的最大值;

    (2)数列{an}前n项和Sn取最大值时的n.

    解:(1)方法一:∵an+1-an=［-(n+1)2+9(n+1)+10］-(-n2+9n+10)=-2(n-4),

        当n＜4时,an+1＞an;

        当n＞4时,an+1＜an;

        当n=4时,an+1=an,

        即a1＜a2＜a3＜a4=a5＞a6＞….

    ∴n=4或n=5时,an最大,此时a4=a5=30.

        方法二:an=-n2+9n+10对应函数y=-x2+9x+10(x＞0),

        其图象的对称轴为x=,易确定n=4或n=5时,an最大,最大值为30.

    (2)∵an对应函数y=-x2+9x+10,当y≥0时有-1≤x≤10,

    ∴当1≤n≤10时,an≥0;当n＞10时,an＜0,

        即有S1＜S2＜S3＜…＜S9=S10＞S11＞S12＞…,

        故Sn取到最大值时的n为9或10.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下列五个命题：
    ①在三角形ABC中，若A＞B则sinA＞sinB；
    ②若数列{bn}的前n项和Sn=n2+2n+1．则数列{bn}从第二项起成等差数列；
    ③已知Sn是等差数列{an}的前n项和，若S7＞S8则S9＞S8；
    ④已知等差数列{an}的前n项和为Sn，若a5=5a3则
    S9S5
    =9；
    ⑤若{an}是等比数列，且Sn=3n+1+r，则r=-1；
    其中正确命题的序号为：
    ①②④
    ①②④
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    等差数列{an}中，公差d≠0，已知数列ak1，ak2，ak3…akn…是等比数列，其中k1=1，k2=7，k3=25．
    （1）求数列{kn}的通项公式kn；
    （2）若a1=9，bn=
    1
    		log3akn+
    		log3(kn+2)
    （n∈N+），Sn是数列{bn}的前n项和，求证Sn＜
    n
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=（1+a）|x|（a＞-1，a∈R）．
    （1）若f（x）在（0，+∞）上为增函数，求实数a的取值范围；
    （2）当a=-
    1
    2
    时，记an=n•f（n），数列{an}的前n项和为Sn，求证：
    1
    2
    ≤Sn＜2    ；
    （3）当a=2且x∈[m，n]，f（x）∈[1，9]时，探求
    m2+n2-2m
    n+1
    的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等差数列{an}中，前n项和Sn=n2-15n，则使Sn有最小值的n是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2014届辽宁沈阳四校协作体高二上学期期中考试理数学试卷（解析版） 题型：解答题

    (本小题满分12分)

    已知Sn为数列{an}的前n项和，a1=9,Sn=n2an-n2(n-1),设bn=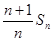

    (1)求证：bn-bn-1="n" (n≥2，n∈N).

    (2)求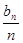的最小值.

     

    查看答案和解析>>

    同步练习册答案