已知函数f(x)=$\left\{\begin{array}{l}{1-{2}^{x}.x≤0}\\{lo{g} {2}x.x＞0}\end{array}\right.$则f=$\frac{7}{8}$．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

19．已知函数f（x）=$\left\{\begin{array}{l}{1-{2}^{x}，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$则f（f（$\frac{1}{8}$））=$\frac{7}{8}$．

分析由分段函数性质，先求出f（$\frac{1}{8}$）=$lo{g}_{2}\frac{1}{8}$=-3，再计算f（f（$\frac{1}{8}$））．

解答解：∵函数f（x）=$\left\{\begin{array}{l}{1-{2}^{x}，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，
∴f（$\frac{1}{8}$）=$lo{g}_{2}\frac{1}{8}$=-3，
∴f（f（$\frac{1}{8}$））=f（-3）=1-2^-3=$\frac{7}{8}$．
故答案为：$\frac{7}{8}$．

点评本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

练习册系列答案

中考新航标初中重点知识总复习指导系列答案

金点新课标同步精练系列答案

教材精析精练字词句篇系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

16．设二次函数f（x）=-$\frac{1}{2}$x²+m图象的顶点为C，与x轴的交点分别为A、B．若△ABC的面积为8$\sqrt{2}$．
（1）求m的值；
（2）求函数f（x）在区间[-1，2]上的最大值与最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．已知等差数列{a_n}满足：a₃=7，a₅+a₇=26，{a_n}的前n项和为S_n
（Ⅰ）求a_n及S_n
（Ⅱ）令b_n=$\frac{1}{{{a}_{n}}^{2}-1}$（n∈N^*），若数列{b_n}的前n项和为T_n，证明：$\frac{1}{8}≤{T_n}＜\frac{1}{4}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

7．若a∈N，又三点A（a，0），B（0，a+4），C（1，3）共线，则a=2．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．

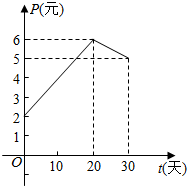某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在图中的两条线段上（如图）．该股票在30天内（包括第30天）的日交易量Q（万股）与时间t（天）的函数关系式为Q=40-t（0≤t≤30且t∈N）．
（1）根据提供的图象，求出该种股票每股的交易价格P（元）与时间t（天）所满足的函数关系式；
（2）用y（万元）表示该股票日交易额（日交易额=日交易量×每股的交易价格），写出y关于t的函数关系式，并求出这30天中第几天日交易额最大，最大值为多少．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．已知函数$f（x）=1-\frac{2}{{{2^x}+1}}$．
（1）求证f（x）是奇函数；
（2）试判断f（x）的单调性并证明．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．