
 在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为| 5 | 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 9 |
| C | 1 2 |
| C | 1 2 |
| 20 |
| 81 |
| 16 |
| 81 |
| ζ | 2 | 4 | 6 | ||||||
| P |
|
|
|
| 5 |
| 9 |
| 20 |
| 81 |
| 16 |
| 81 |
| 266 |
| 81 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)第十六届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
(1)根据以上数据完成下面列联表:
(2)根据列联表的独立性检验,能否有![]() 把握认为性别与喜爱运动有关。
把握认为性别与喜爱运动有关。
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式: ![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三百题集理科数学试卷(解析版)(四) 题型:解答题
2010年11月广州成功举办了第十六届亚运会。在华南理工大学学生会举行的亚运知识有奖问答比赛中,甲、乙、丙同时回答一道有关亚运知识的问题,已知甲回答对这道题目的概率是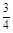 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是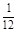 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是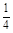 .
.
(1)求乙、丙两人各自回答对这道题目的概率.
(2)(理)求回答对这道题目的人数的随机变量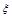 的分布列和期望.
的分布列和期望.
【解析】本试题主要考查了独立事件概率的乘法计算公式的运用。以及对立事件的概率的运用。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com