
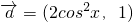 ,
, =(1,
=(1,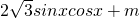 )(x∈R,m∈R,m是常数)且
)(x∈R,m∈R,m是常数)且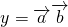 .
. 时,f(x)的最大值为4,求m的值;
时,f(x)的最大值为4,求m的值;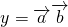 =2cos2x+2
=2cos2x+2 sinxcosx+m=cos2x+
sinxcosx+m=cos2x+ sin2x+m+1=2sin(2x+
sin2x+m+1=2sin(2x+ )+m+1.
)+m+1. )+m+1.
)+m+1. )+m+1的最大值为4,故m=1.
)+m+1的最大值为4,故m=1. =π,令 2kπ+
=π,令 2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,解得 kπ+
,k∈z,解得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z,
,k∈z, ,kπ+
,kπ+ ],k∈z.
],k∈z. )+m+1.
)+m+1. )+m+1的最大值为4,由此求得m的值.
)+m+1的最大值为4,由此求得m的值. =π,令 2kπ+
=π,令 2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈z,求出x的范围,即可求得f(x)的单调减区间.
,k∈z,求出x的范围,即可求得f(x)的单调减区间.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com