
【题目】在平面直角坐标系![]() 中,已知圆C经过
中,已知圆C经过![]() ,
,![]() ,
,![]() (
(![]() )三点,M是线段
)三点,M是线段![]() 上的动点,
上的动点,![]() ,
,![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交y轴于点E,
交y轴于点E,![]() 交圆C于P、Q两点.
交圆C于P、Q两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 是使
是使![]() 恒成立的最小正整数
恒成立的最小正整数
①求![]() 的值; ②求三角形
的值; ②求三角形![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】
(1)求出圆的标准方程,设直线![]() 的方程
的方程![]() ,利用
,利用![]() ,结合圆心到直线的距离分析可得
,结合圆心到直线的距离分析可得![]() ,解可得
,解可得![]() 的值,验证直线与
的值,验证直线与![]() 轴有无交点,即可得答案;
轴有无交点,即可得答案;
(2)①设![]() ,由点
,由点![]() 在线段
在线段![]() 上,得
上,得![]() ,由
,由![]() ,得
,得![]() ,结合题意,线段
,结合题意,线段![]() 与圆
与圆![]() 至多有一个公共点,分析可得
至多有一个公共点,分析可得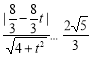 ,分析可得
,分析可得![]() 的值,
的值,
②由①的结论,分直线的斜率存在与不存在2种情况讨论,用![]() 表示三角形
表示三角形![]() 的面积,结合二次函数的性质分析可得答案.
的面积,结合二次函数的性质分析可得答案.
解:(1)由题意可知,圆C的直径为![]() ,
,
所以圆C方程为:![]() ,设
,设![]() 方程为:
方程为:![]() ,则
,则![]() ,
,
解得![]() ,
,![]() ,当
,当![]() 时,直线
时,直线![]() 与y轴无交点,不合题意,舍去.
与y轴无交点,不合题意,舍去.
所以,![]() 时直线
时直线![]() 的方程为
的方程为![]() .
.
(2)①设![]() ,由点
,由点![]() 在线段
在线段![]() 上,则有
上,则有![]() ,即
,即![]() .
.
由![]() ,则有
,则有![]()
依题意知,线段![]() 与圆
与圆![]() 至多有一个公共点,
至多有一个公共点,
故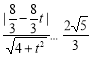 ,解可得
,解可得![]() 或
或![]() ,
,
因为![]() 是使
是使![]() 恒成立的最小正整数,所以
恒成立的最小正整数,所以![]() ;
;
②由①的结论,圆![]() 的方程为
的方程为![]() .
.
分2种情况讨论:
![]() 当直线
当直线![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,此时,
,此时,![]() ;
;
![]() 当直线
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,
,![]() ,
,
则![]() 的方程为
的方程为![]() ,
,
点![]() ,所以
,所以![]() ,
,
又圆心到![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
故![]() ,
,
又由![]() ,
,
故求三角形![]() 的面积的最小值为
的面积的最小值为![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)判断函数![]() 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)是否存在实数![]() ,使得当
,使得当![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某权威机构发布了2014年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):

(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】鲁班锁是中国古代传统土木建筑中常用的固定结合器,也是广泛流传于中国民间的智力玩具,它起源于古代中国建筑首创的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看上去是严丝合缝的十字几何体,其上下左右前后完全对称,十分巧妙.鲁班锁的种类各式各样,其中以最常见的六根和九根的鲁班锁最为著名.九根的鲁班锁由如图所示的九根木榫拼成,每根木榫都是由一根正四棱柱状的木条挖一些凹槽而成.若九根正四棱柱底面边长均为1,其中六根最短条的高均为3,三根长条的高均为5,现将拼好的鲁班锁放进一个球形容器内,使鲁班锁最高的三个正四棱柱形木榫的上下底面顶点分别在球面上,则该球形容器的表面积(容器壁的厚度忽略不计)的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a,b的值分别为( )

A.0.27,78B.54,0.78C.27,0.78D.54,78
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷项等差数列![]() 的公差为
的公差为![]() ,前n项和为
,前n项和为![]() ,则下列四个说法中正确的个数是( )
,则下列四个说法中正确的个数是( )
①若![]() ,则数列
,则数列![]() 有最大项;②若数列
有最大项;②若数列![]() 有最大项,则
有最大项,则![]() ;
;
③若数列![]() 是递增数列,则对任意的
是递增数列,则对任意的![]() ,均有
,均有![]() ;
;
④若对任意的![]() ,均有
,均有![]() ,则数列
,则数列![]() 是递增数列.
是递增数列.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】费马点是指三角形内到三角形三个顶点距离之和最小的点。当三角形三个内角均小于![]() 时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为
时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为![]() 。根据以上性质,函数
。根据以上性质,函数![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com