
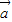 =(sin2x,1),向量
=(sin2x,1),向量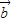 =(
=( ,1),函数f(x)=λ
,1),函数f(x)=λ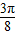 ,
,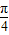 ]且当λ≠0时,求函数f(x)的单调递减区间;
]且当λ≠0时,求函数f(x)的单调递减区间; ,
,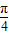 ]且当λ≠0时,∴
]且当λ≠0时,∴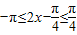 ,对λ>0,λ<0分类讨论求出函数的单调减区间.
,对λ>0,λ<0分类讨论求出函数的单调减区间.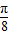 个单位,图象上每个点的纵坐标扩大为原来的
个单位,图象上每个点的纵坐标扩大为原来的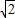 倍,
倍,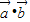 =(sin2x,1)•(
=(sin2x,1)•(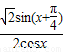 ,1)=sinx(sinx+cosx)+1
,1)=sinx(sinx+cosx)+1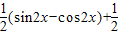 =
=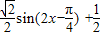

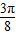 ,
,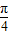 ]∴
]∴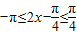
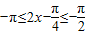 得单调递减区间为
得单调递减区间为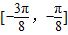
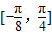
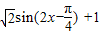 ,变换过程如下:
,变换过程如下: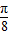 个单位可得函数y=
个单位可得函数y=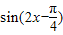 的图象.
的图象.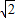 倍,而横坐标保持不变,可得函数
倍,而横坐标保持不变,可得函数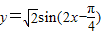 的图象.
的图象.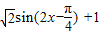 的图象.
的图象.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
| a |
| π |
| 6 |
| π |
| 6 |
| b |
| π |
| 6 |
| π |
| 6 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| π |
| 8 |
| π |
| 8 |
| b |
| π |
| 8 |
| a |
| b |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| π |
| 2 |
| a |
| b |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:辽宁省大连市、沈阳市2012届高三第二次联合考试数学文科试题 题型:044
已知向量m=(sin2+![]() ,sinx),n=(
,sinx),n=(![]() cos2x-
cos2x-![]() sin2x,2sinx),函数f(x)=m·n.
sin2x,2sinx),函数f(x)=m·n.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若![]() ,求函数f(x)值域.
,求函数f(x)值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com