分析:(1)连接AB
1则易得点M是AB
1的中点,点N是B
1C的中点故根据中位线定理可得MN∥AC然后利用线面平行的判定定理即可得证.
(2)(法一)作AD⊥A
1C,交A
1C于点D,由条件知点D是A
1C中点,连接BD则根据题中条件可得AB⊥AC,AB⊥AA
1,再结合线面垂直的判定定理可得AB⊥面ACC
1A
1故AB⊥A
1C所以A
1C⊥面ABD所以BD⊥A
1C故∠ADB为二面角A-A
1C-B的平面角然后再解三角形求出cos∠ADB.
(法二)易得AB⊥AC,AB⊥AA
1,AC⊥AA
1,故可建立如图所示的空间直角坐标系然后求出平面AA
1C的法向量
,平面A
1BC的法向量
然后利用向量的夹角公式cos<
,>=
即可求解.
解答:
(1)证明:连接AB
1∵四边形A
1ABB
1是矩形,点M是A
1B的中点
∴点M是AB
1的中点
∵点N是B
1C的中点
∴MN∥AC
∵MN?平面ABC,AC?平面ABC
∴MN∥平面ABC
(Ⅱ)解:(方法一)如图作AD⊥A
1C,交A
1C于点D,由条件知点D是A
1C中点,连接BD
∵AB=1,AC=AA
1=
,BC=2

∴AB
2+AC
2=BC
2∴AB⊥AC
∵AB⊥AA
1,AA
1∩AC=A
∴AB⊥面ACC
1A
1∴AB⊥A
1C
∴A
1C⊥面ABD
∴BD⊥A
1C
∴∠ADB为二面角A-A
1C-B的平面角
在Rt△AA
1C中,AD=
=∵BC=BA
1=2,A
1C=6,在等腰三角形CBA
1中D是A
1C中点,BD=
∴△ABD中,∠BAD=90°
∵在Rt△ABD中,tan∠ADB=
=∴二面角A-A
1C-B的余弦值是
(方法二)∵三棱锥ABC-A
1B
1C
1为直三棱锥
∴AB⊥AA
1,AC⊥AA
1∵AB=1,AC=
,BC=2
∴AB
2+AC
2=BC
2∴AB⊥AC
如图建立空间直角坐标系则A(0,0,0),B(0,1,0),C(
,0,0),A
1(0,0,
)
如图可取
=
=(0,1,0)为平面AA
1C的法向量
设平面A
1BC的法向量为
=(m,l,n)则
•= 0,
•=0又
=(,-1,0),
=(,0,-)∴
∴l=
m,n=m不妨取m=1则
=(1,,1)∴cos<
•>=
∴二面角A-A
1C-B的余弦值是
点评:本题主要考查了线面平行的证明以及二面角的求解,属必考题,较难.解题的关键是透彻理解线面平行的判定定理和二面角的定义同时要注意空间向量法在求解二面角中点应用!

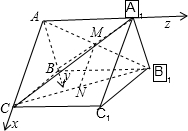
 如图,在直三棱柱ABC-A1B1C1中,点M是A1B中点,点N是B1C的中点,连接MN.
如图,在直三棱柱ABC-A1B1C1中,点M是A1B中点,点N是B1C的中点,连接MN. (1)证明:连接AB1
(1)证明:连接AB1







